probability space and measurable maps

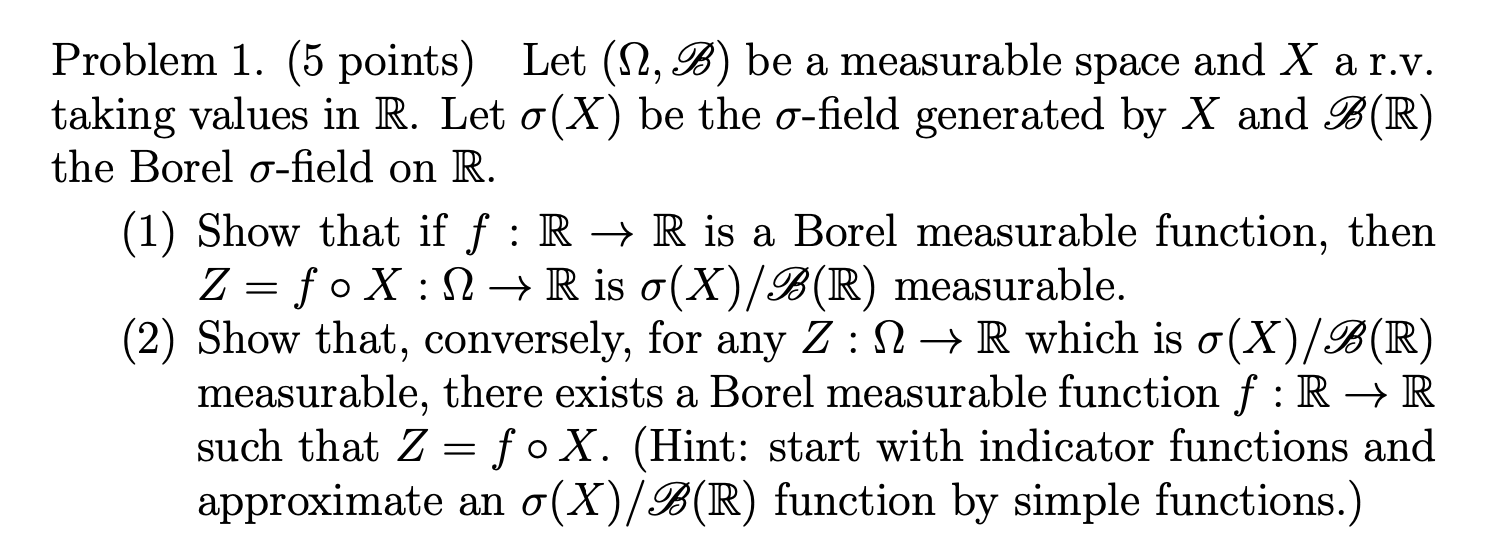
Problem 1. (5 points) Let (Q, Q) be a measurable space and X a r.v. taking values in R. Let 0(X) be the aeld generated by X and %(R) the Borel aeld on R. (1) Show that if f : R > R is a Borel measurable function, then Z = f o X : 9 > IR is a(X)/.%'(R) measurable. (2) Show that, conversely, for any Z : 9 > R which is 0(X)/.%'(R) measurable, there exists a Borel measurable function f : R > R such that Z = f o X. (Hint: start With indicator functions and approximate an 0(X)/.%(R) function by simple functions.)