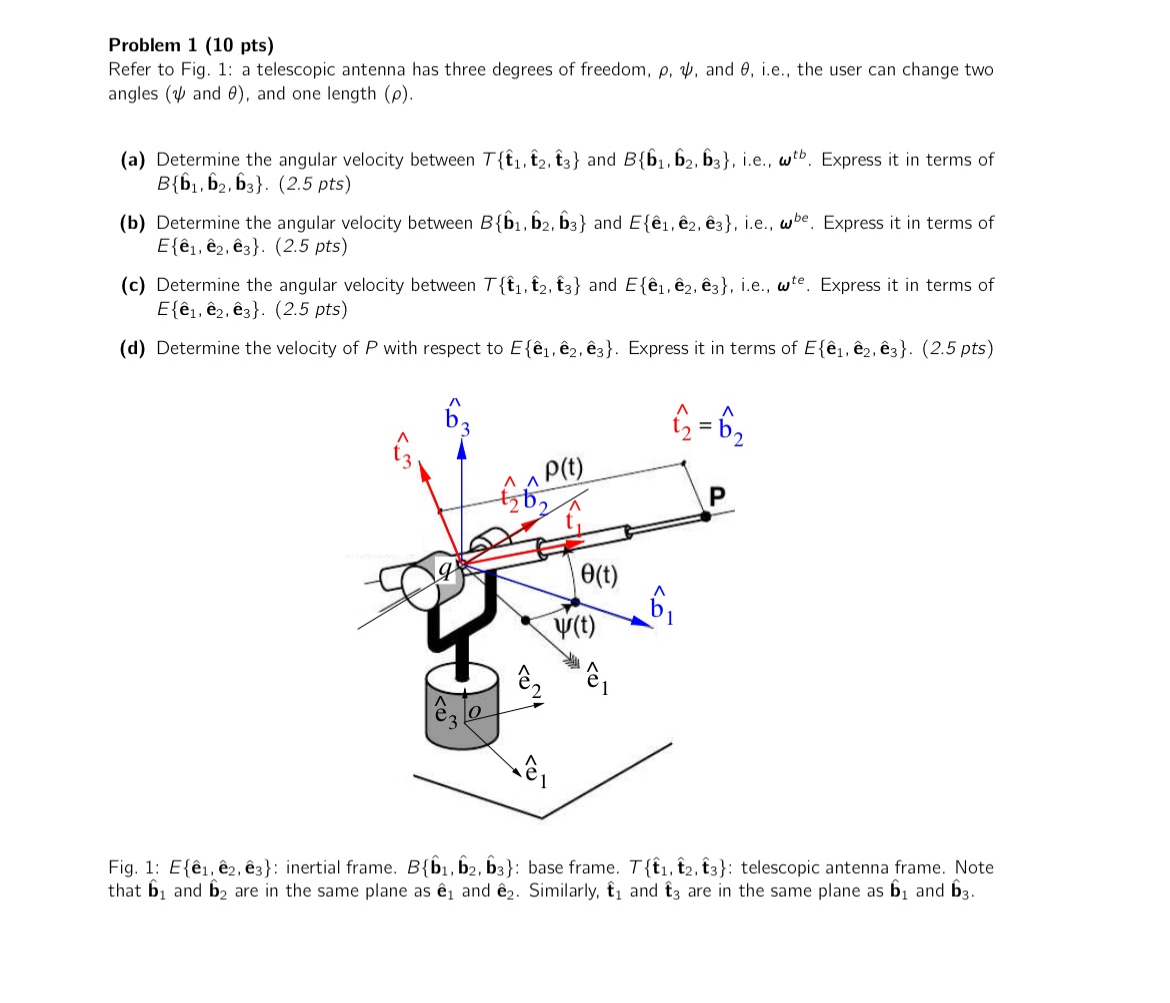
Question: Problem 1 ( 1 0 pts ) Refer to Fig. 1 : a telescopic antenna has three degrees of freedom, , , and , i
Problem pts
Refer to Fig. : a telescopic antenna has three degrees of freedom, and ie the user can change two angles and and one length
a Determine the angular velocity between hathat and hathat ie Express it in terms of pts
b Determine the angular velocity between hathat and hathat ie Express it in terms of hathat pts
c Determine the angular velocity between hathat and hathat ie Express it in terms of hathat pts
d Determine the velocity of with respect to hathat Express it in terms of hathat pts
Fig. : hathat : inertial frame. hathat : base frame. hathat : telescopic antenna frame. Note that hat and hat are in the same plane as hat and hat Similarly, hat and hat are in the same plane as hat and hat
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


