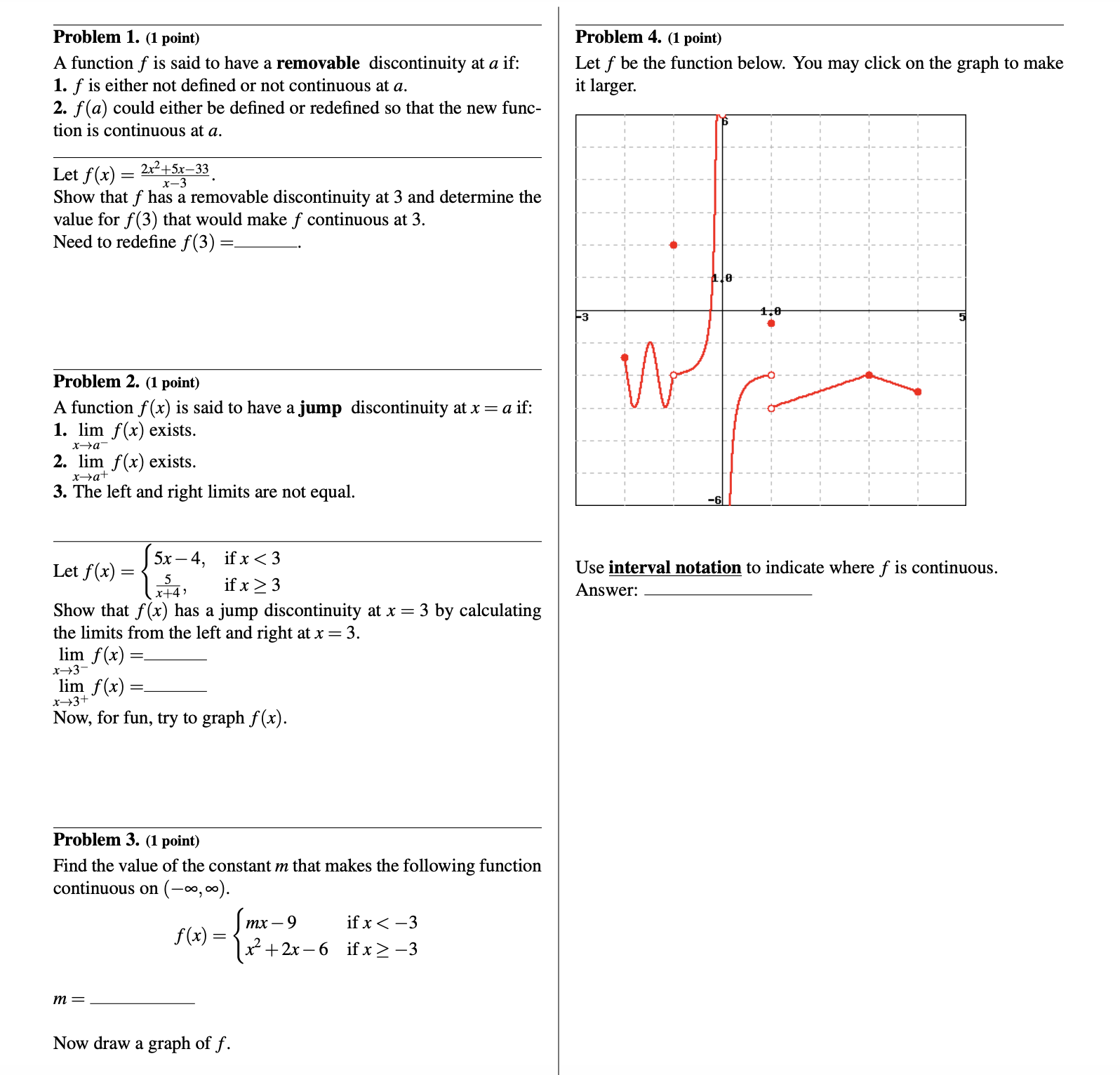
Problem 1. (1 point) A function f is said to have a removable discontinuity at a if: 1. f is either not defined or not continuous at a. 2. f(a) could either be defined or redefined so that the new func- tion is continuous at a. Let f(x) = 274533, Show that f has a removable discontinuity at 3 and determine the value for f(3) that would make f continuous at 3. Need to redefine f(3) = Problem 2. (1 point) A function f(x) is said to have a jump discontinuity at x = a if: 1. lim f(x) exists. X=ra 2. lim f(x) exists. xat 3. The left and right limits are not equal. Sx4, ifx3 e g x> Show that f(x) has a jump discontinuity at x = 3 by calculating the limits from the left and right at x = 3. lim f(x)= x3" lim f(x)= x3t f( ) Now, for fun, try to graph f(x). Problem 3. (1 point) Find the value of the constant m that makes the following function continuous on (eo, o). mx9 _{f+h6 ifx -3 m= Now draw a graph of f. Problem 4. (1 point) Let f be the function below. You may click on the graph to make it larger. Use interval notation to indicate where f is continuous.