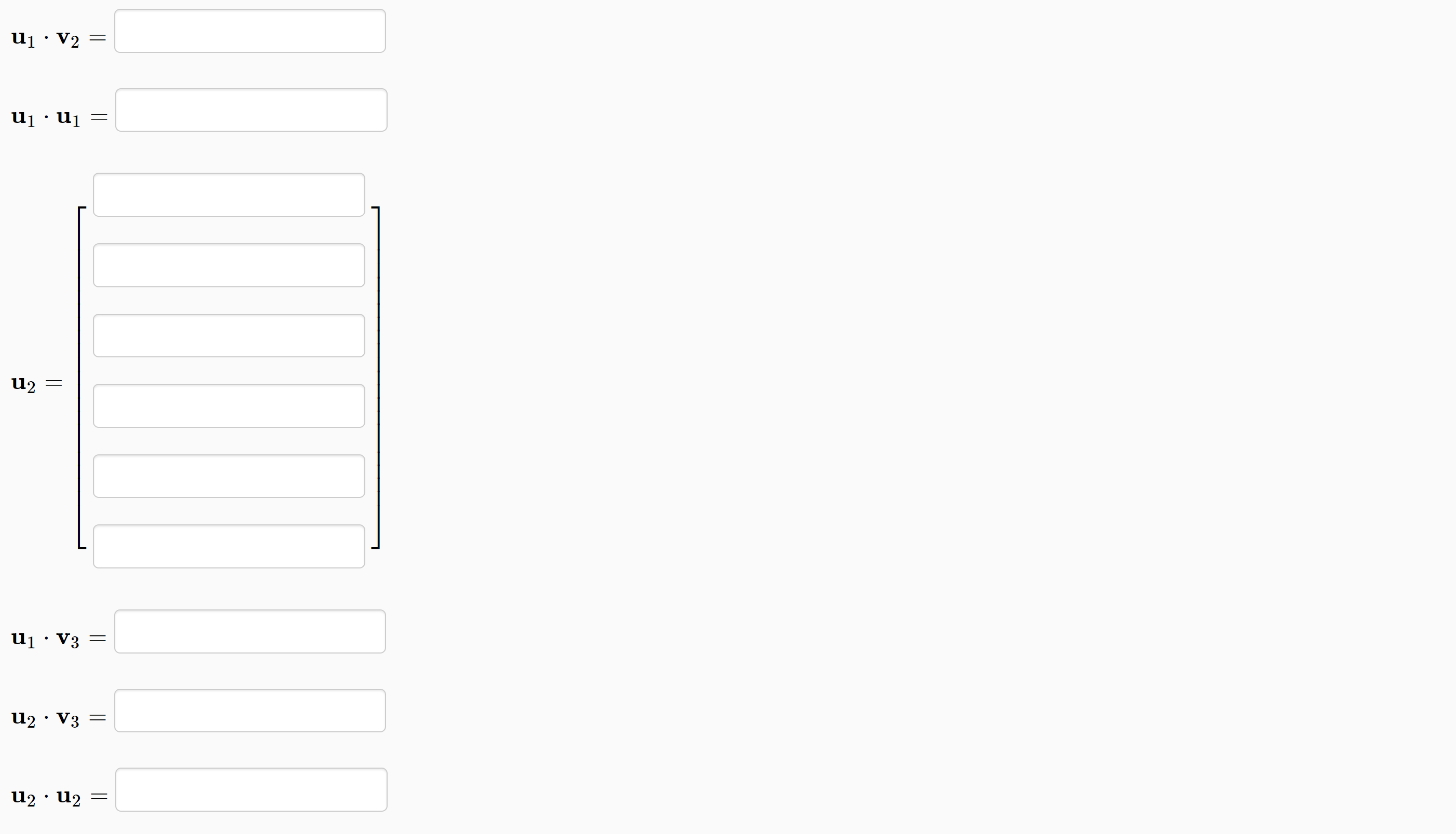
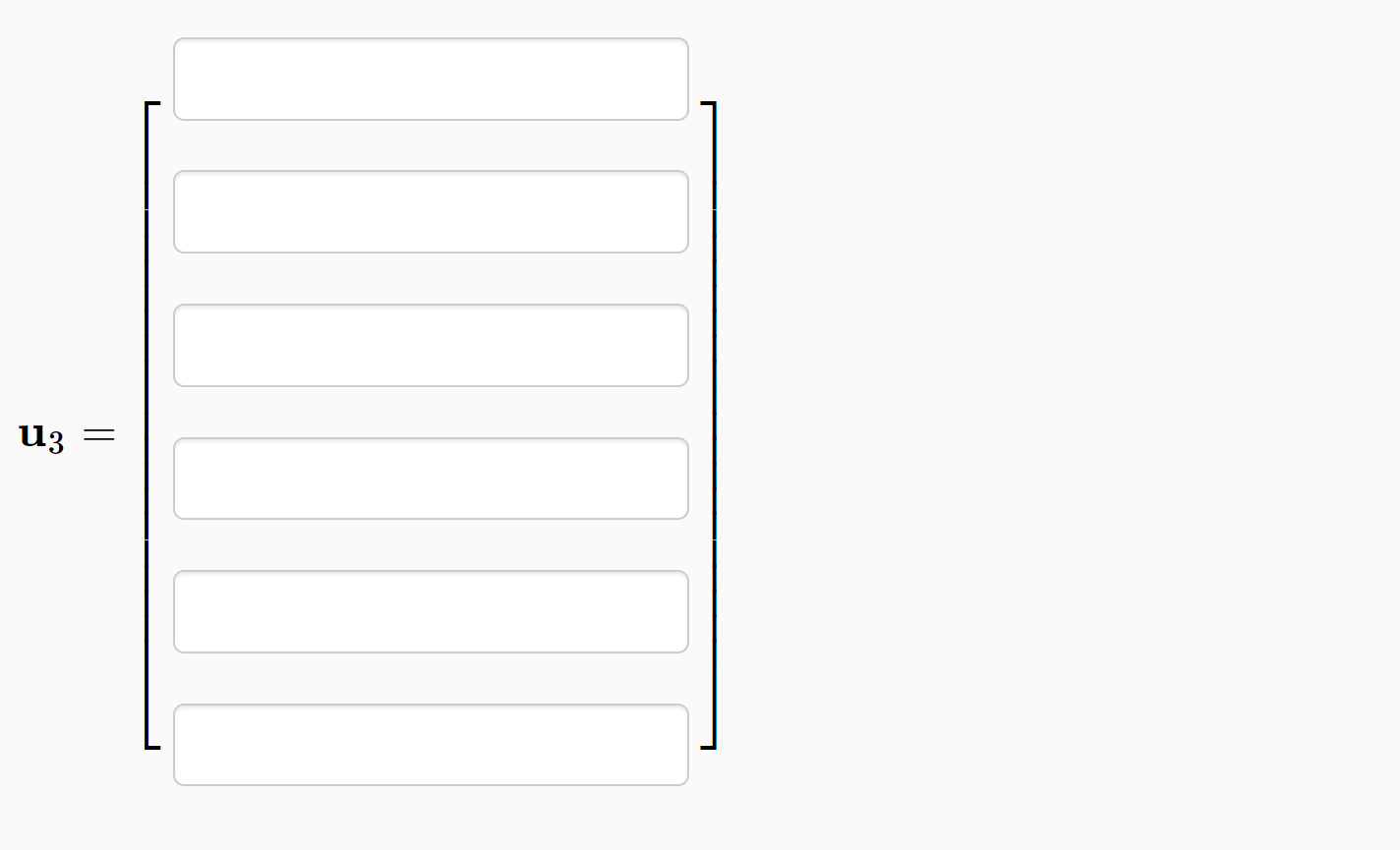
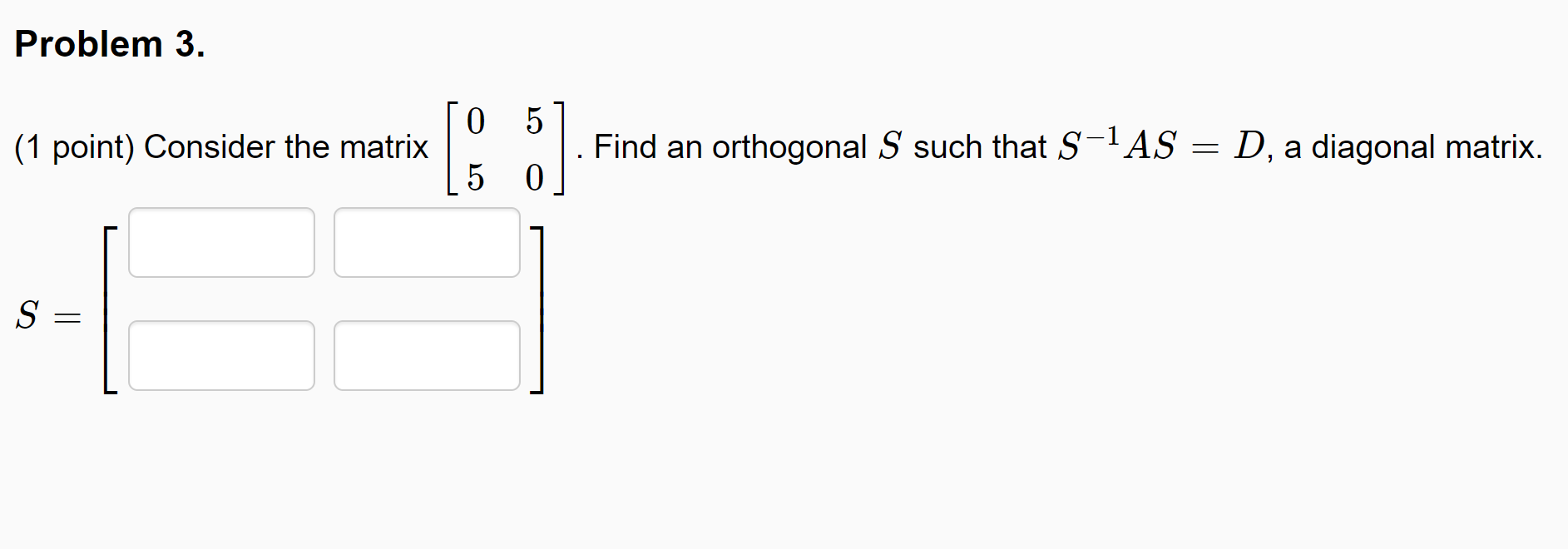
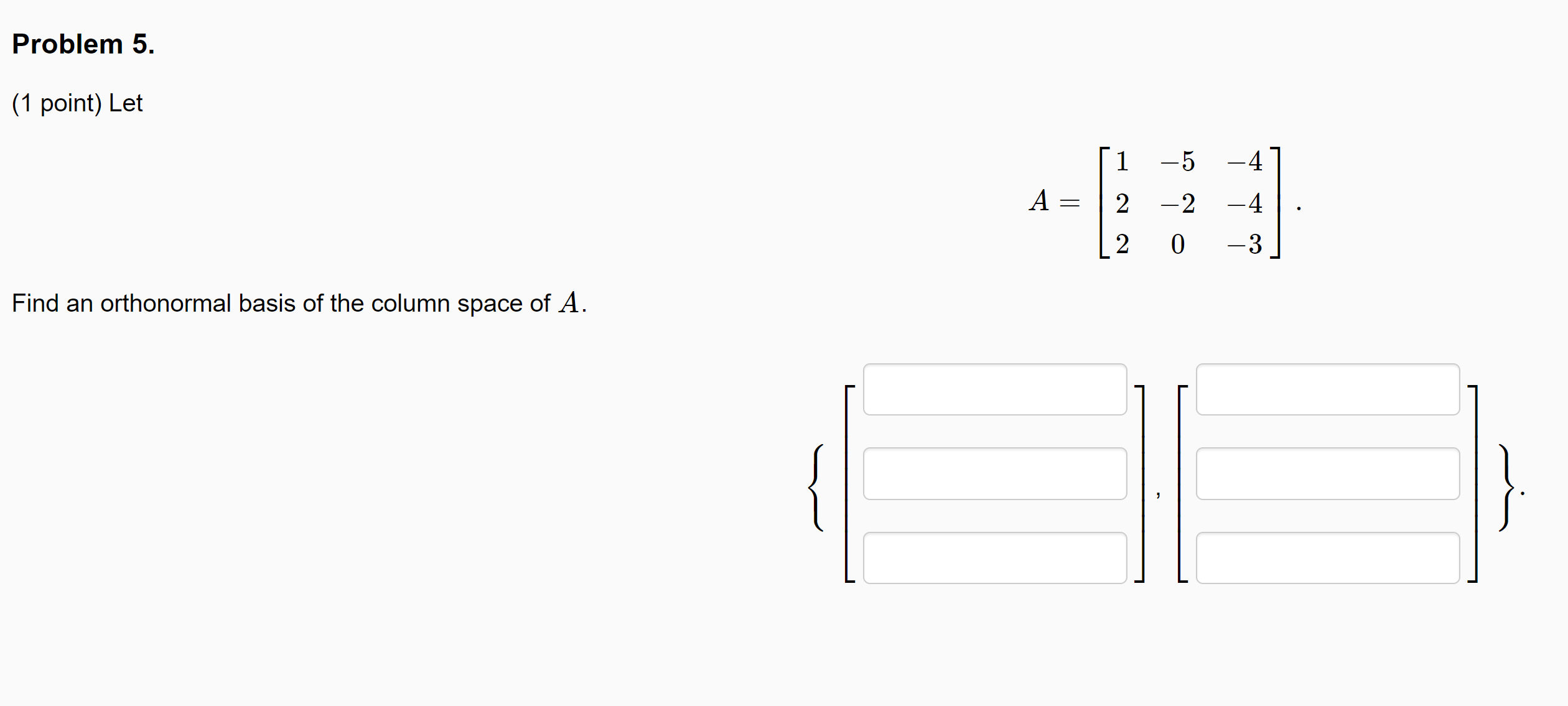
Problem 1. (1 point) Let 1 l 2 5 0 0 v1 0 ,V2: 5 ,andV3: 0 *3 2 72 0 0 1 4 4 5 Use the Gram-Schmidt procedure to produce an orthogonal set with the same span. (Hint: If you have unlimited submissions, it might be useful to submit to check your answer for each vector uj before continuing.) Note: The uj must be given in the same order as provided by the standard procedure. Problem 2. (1 point) Let 0 1 2 0 0 11 v1 4 ,v2= 2 ,andva= 2 9 0 0 3 4 3 0 8 0 Use the Gram-Schmidt procedure to produce an orthogonal set with the same span. (Hint: If you have unlimited submissions, it might be useful to submit to check your answer for each vector uj before continuing.) The uj must be given in the same order as provided by the stand ard procedure. Problem 3. 0 5 5 0] . Find an orthogonal S such that S'lAS' : D, a diagonal matrix. (1 point) Consider the matrix [ 3: Problem 4. (1 point) The matrix 3 0 12 A = 0 3 0 2 0 7 has two real eigenvalues, A1 = 3 of multiplicity 2, and A2 = 1 of multiplicity 1. Find an orthonormal basis for the eigenspace corresponding to A1. Problem 5. (1 point) Let Find an orthonormal basis of the column space of A. 1 5 4 2 2 4 2 0 3 Problem 6. (1 point) Find the eigenvalues /1 2 and associated orthonormal eigenvectors of the symmetric matrix 4 2 O N -4 O A = NOO O OO 0 2 A1 = has associated orthonormal eigenvectors 12 = has associated orthonormal eigenvectors Note: The eigenvectors above form an orthonormal eigenbasis for A