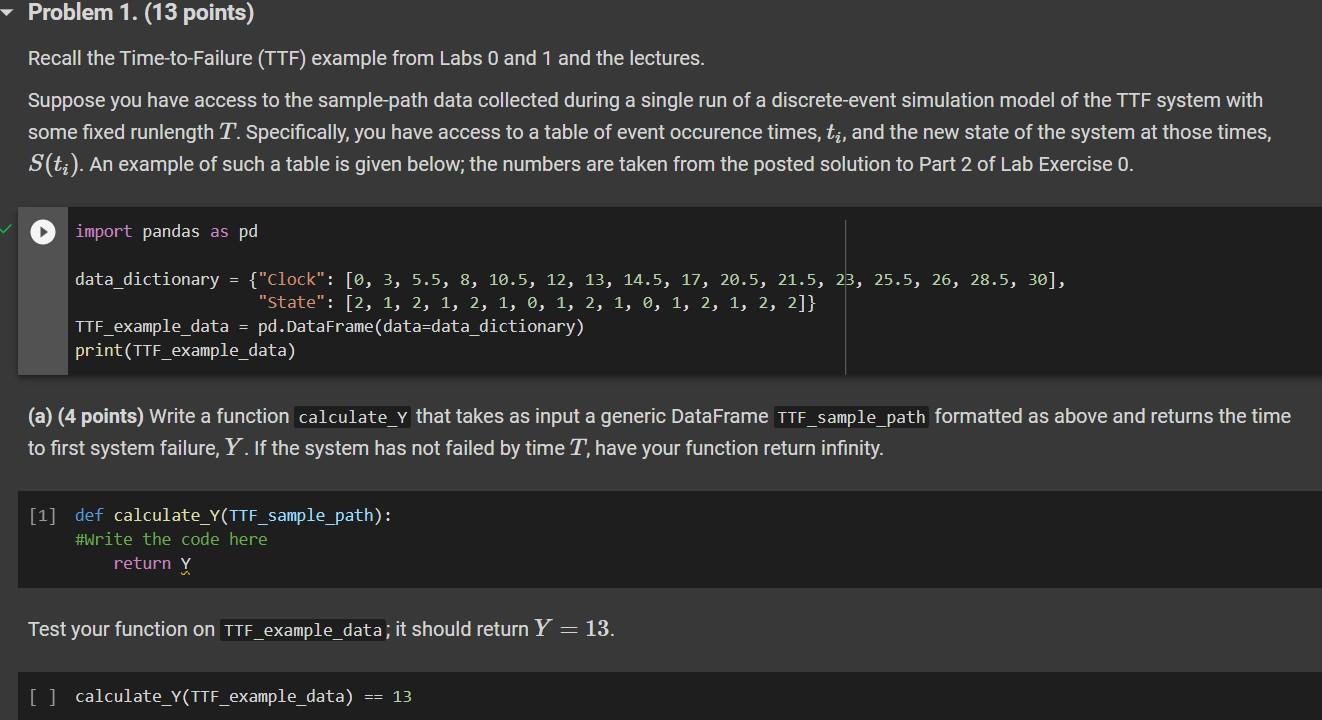
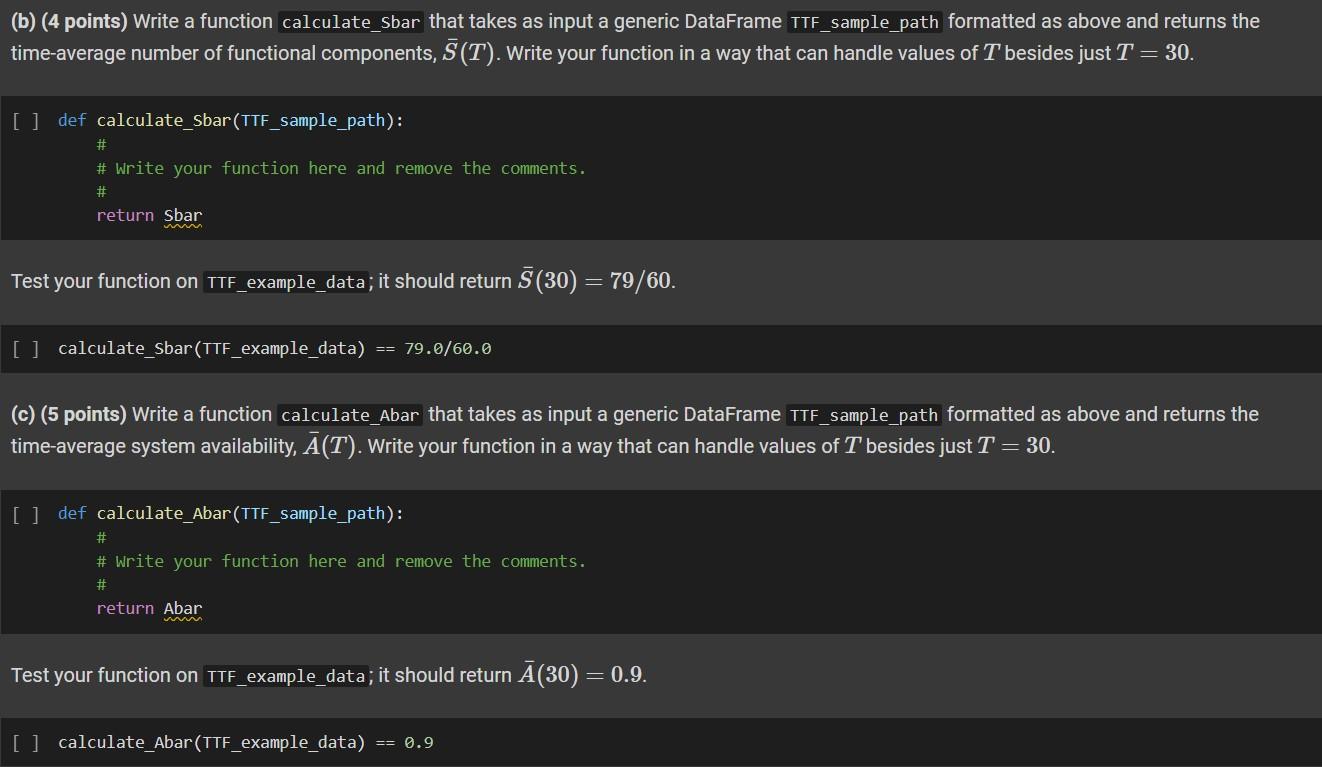
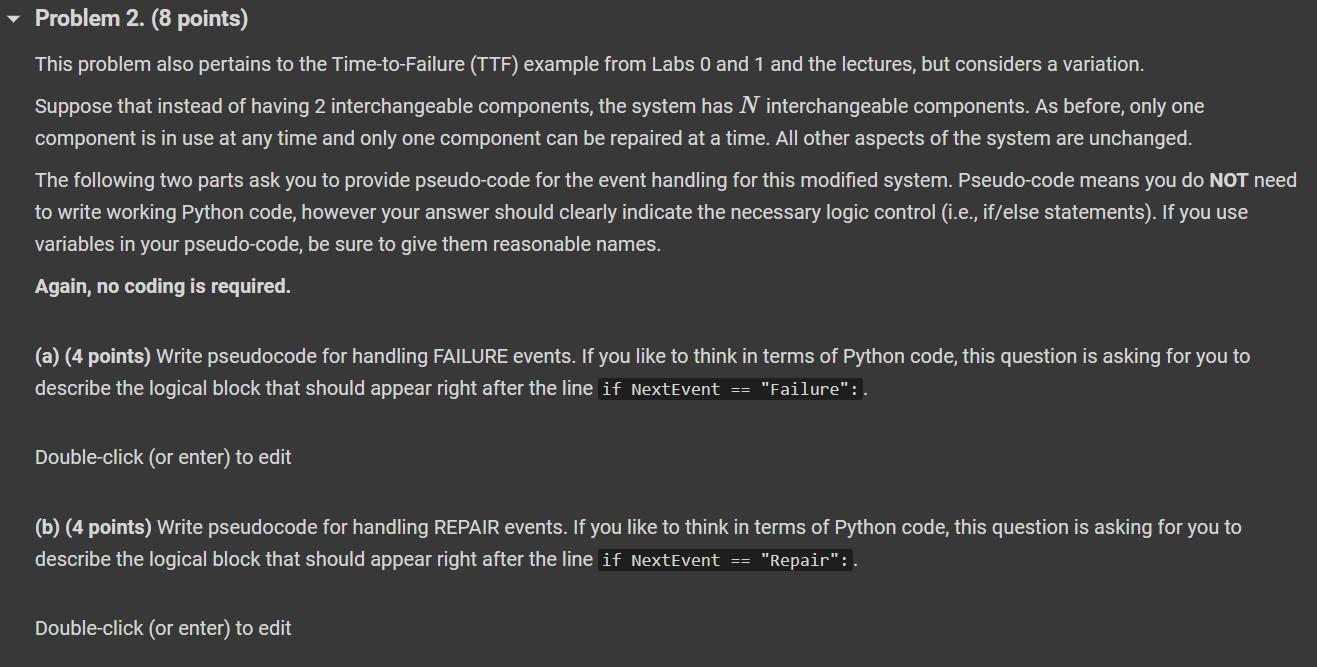
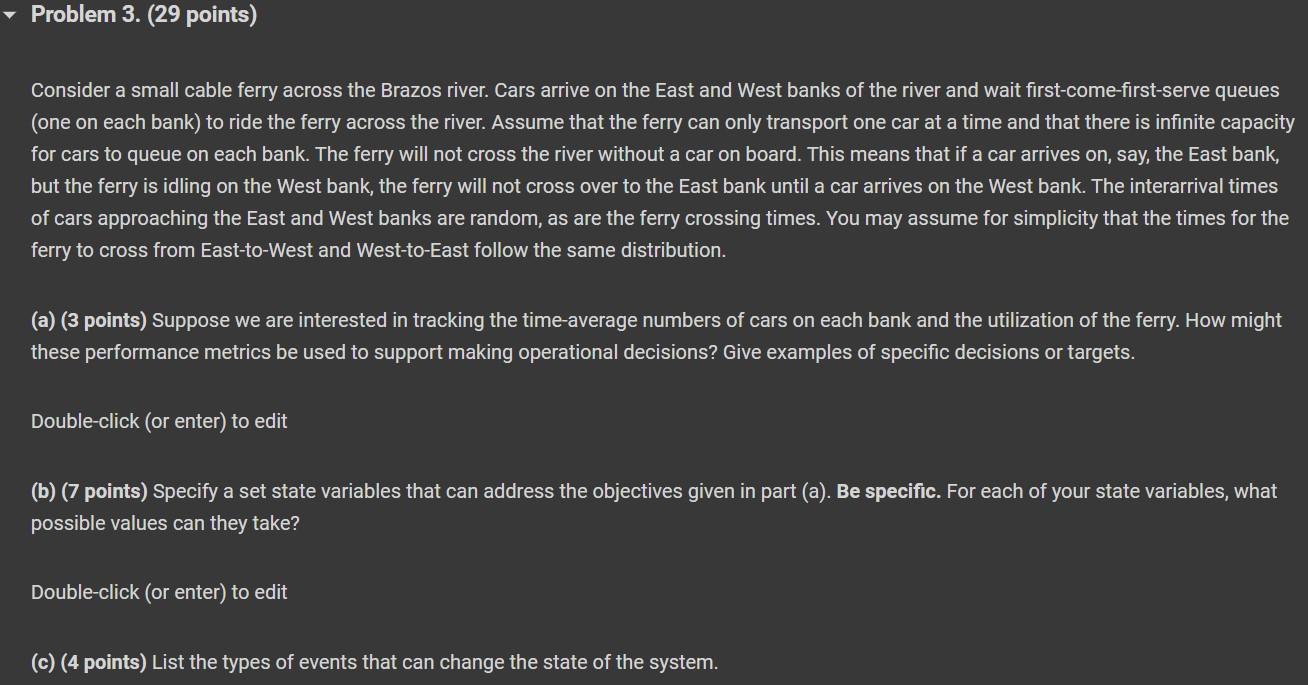
Problem 1. (13 points) Recall the Time-to-Failure (TTF) example from Labs 0 and 1 and the lectures. Suppose you have access to the sample-path data collected during a single run of a discrete-event simulation model of the TTF system with some fixed runlength T. Specifically, you have access to a table of event occurence times, ti, and the new state of the system at those times, S(ti). An example of such a table is given below; the numbers are taken from the posted solution to Part 2 of Lab Exercise 0. import pandas as pd (a) (4 points) Write a function calculate_Y that takes as input a generic DataFrame TTF_sample_path formatted as above and returns the time to first system failure, Y. If the system has not failed by time T, have your function return infinity. [1] def calculate_Y(TTF_sample_path): \#Write the code here return Y Test your function on TTF_example_data; it should return Y=13. [ ] calculate_Y(TTF_example_data )=13 (b) (4 points) Write a function calculate_sbar that takes as input a generic DataFrame TTF_sample_path formatted as above and returns the time-average number of functional components, S(T). Write your function in a way that can handle values of T besides just T=30. [ ] def calculate_Sbar(TTF_sample_path): # \# Write your function here and remove the comments. return s sbar Test your function on TTF_example_data; it should return S(30)=79/60. [ ] calculate_Sbar ( TTF_example_data )=79.0/60.0 (c) (5 points) Write a function calculate_Abar that takes as input a generic DataFrame TTF_sample_path formatted as above and returns the time-average system availability, A(T). Write your function in a way that can handle values of T besides just T=30. [ ] def calculate_Abar(TTF_sample_path): \# \# Write your function here and remove the comments. return Abar Test your function on TTF_example_data; it should return A(30)=0.9. This problem also pertains to the Time-to-Failure (TTF) example from Labs 0 and 1 and the lectures, but considers a variation. Suppose that instead of having 2 interchangeable components, the system has N interchangeable components. As before, only one component is in use at any time and only one component can be repaired at a time. All other aspects of the system are unchanged. The following two parts ask you to provide pseudo-code for the event handling for this modified system. Pseudo-code means you do NOT need to write working Python code, however your answer should clearly indicate the necessary logic control (i.e., if/else statements). If you use variables in your pseudo-code, be sure to give them reasonable names. Again, no coding is required. (a) (4 points) Write pseudocode for handling FAILURE events. If you like to think in terms of Python code, this question is asking for you to describe the logical block that should appear right after the line if NextEvent == "Failure" : . Double-click (or enter) to edit (b) (4 points) Write pseudocode for handling REPAIR events. If you like to think in terms of Python code, this question is asking for you to describe the logical block that should appear right after the line if NextEvent == "Repair": . Double-click (or enter) to edit Problem 3. (29 points) Consider a small cable ferry across the Brazos river. Cars arrive on the East and West banks of the river and wait first-come-first-serve queues (one on each bank) to ride the ferry across the river. Assume that the ferry can only transport one car at a time and that there is infinite capacity for cars to queue on each bank. The ferry will not cross the river without a car on board. This means that if a car arrives on, say, the East bank, but the ferry is idling on the West bank, the ferry will not cross over to the East bank until a car arrives on the West bank. The interarrival times of cars approaching the East and West banks are random, as are the ferry crossing times. You may assume for simplicity that the times for the ferry to cross from East-to-West and West-to-East follow the same distribution. (a) (3 points) Suppose we are interested in tracking the time-average numbers of cars on each bank and the utilization of the ferry. How might these performance metrics be used to support making operational decisions? Give examples of specific decisions or targets. Double-click (or enter) to edit (b) (7 points) Specify a set state variables that can address the objectives given in part (a). Be specific. For each of your state variables, what possible values can they take? Double-click (or enter) to edit (c) (4 points) List the types of events that can change the state of the system. (d) (12 points) For each event type you listed in part (c), describe the event-handling logic. How should the state variables be updated? Under what conditions can a future event be scheduled and of what type? (Since no probability distributions are specified in the problem statement, your logic may contain statements like 'Generate a random river crossing time.')