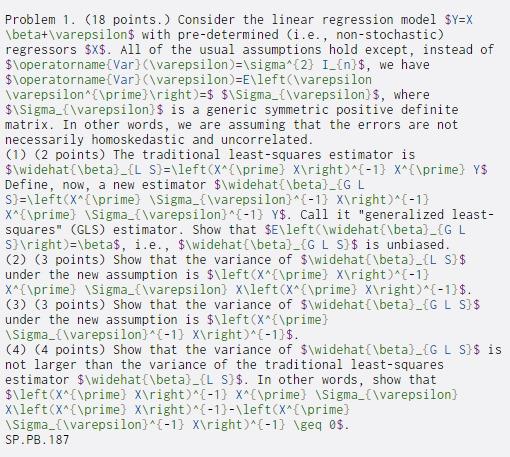
Problem 1. (18 points. Consider the linear regression model $Y=X \beta+\varepsilon$ with pre-determined (i.e., non-stochastic) regressors $X$. All of the usual assumptions hold except, instead of $\operatorname[Var} (\varepsilon)=\sigma^{2} I_{n}$, we have $\operatorname[Var}(\varepsilon)=E\left(\varepsilon \varepsilon"{\prime} ight)=$ $\Sigma_{Warepsilon), where $\Sigma_{\varepsilon}$ is a generic symmetric positive definite matrix. In other words, we are assuming that the errors are not necessarily homoskedastic and uncorrelated. (1) (2 points) The traditional least-squares estimator is $\widehat{\beta}_{L S)=\left(X^{\prime} X ight)^{-1} X^{\prime} Y$ Define, now, a new estimator $\widehat{\beta}_{GL S}=\left(X^{\prime} \Sigma_{\varepsilon}^{-1} X ight)^{-1} X^{\prime} \Sigma_{\arepsilon}^{-1} Y$. Call it "generalized least- squares" (GLS) estimator. Show that $E\left(\widehat{\beta)_{GL S} ight)=\beta$, i.e., $\widehat{\beta}_{G L S $ is unbiased. (2) (3 points) Show that the variance of $\widehat{\beta) (L S} $ under the new assumption is $\left(X^{\prime] X ight)^{-1} X^{\prime} \Sigma_{\varepsilon] X\left(X^{\prime} X ight)^{-1}$. (3) (3 points) Show that the variance of $\widehat[\beta) {GL S}$ under the new assumption is $\left(X^{\prime] \Sigma_{\varepsilon}^{-1} X ight)^{-1}$. (4) (4 points) Show that the variance of $\widehat{\beta) {GL S}$ is not larger than the variance of the traditional least-squares estimator $\widehat{\beta)_{L S]$. In other words, show that $\left(X^{\prime] X ight)^{-1} X^{\prime) \Sigma_{\varepsilon) X\left(X^{\prime] X ight)^{-1}-\left(X^{\prime) \Sigma_{\varepsilon}^{-1} X ight)^{-1} \geq 0$. SP.PB. 187