Problem $1(25$ points$)$

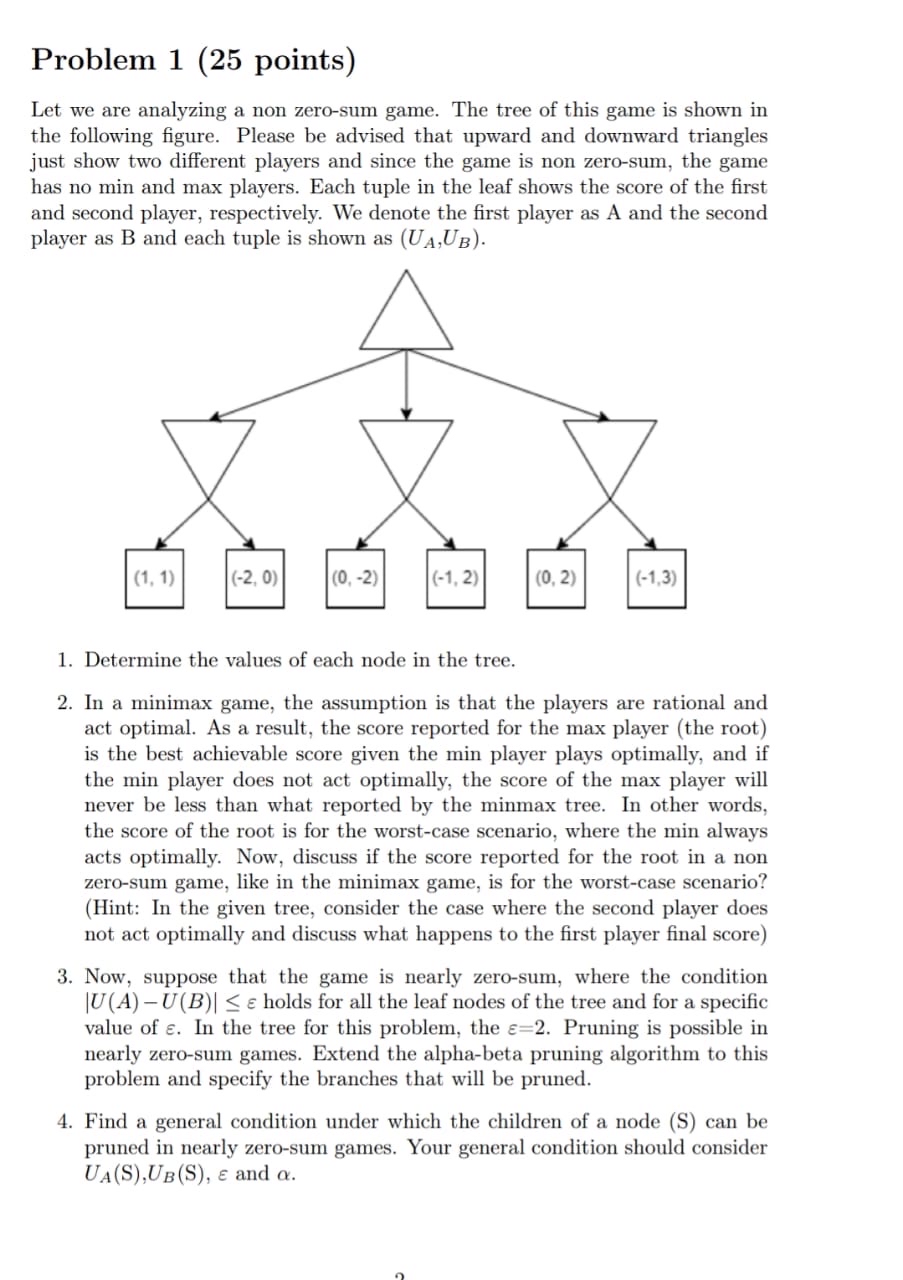
Let we are analyzing a non zero$-$sum game. The tree of this game is shown in the following figure. Please be advised that upward and downward triangles just show two different players and since the game is non zero$-$sum, the game has no min and max players. Each tuple in the leaf shows the score of the first and second player, respectively. We denote the first player as A and the second player as B and each tuple is shown as $(U_A,U_B).$

Determine the values of each node in the tree.

In a minimax game, the assumption is that the players are rational and act optimal. As a result, the score reported for the max player $($the root$)$ is the best achievable score given the min player plays optimally, and if the min player does not act optimally, the score of the max player will never be less than what reported by the minmax tree. In other words, the score of the root is for the worst$-$case scenario, where the min always acts optimally. Now, discuss if the score reported for the root in a non zero$-$sum game, like in the minimax game, is for the worst$-$case scenario? $($Hint: In the given tree, consider the case where the second player does not act optimally and discuss what happens to the first player final score$)$

Now, suppose that the game is nearly zero$-$sum, where the condition $|U(A)-U(B)|$ holds for all the leaf nodes of the tree and for a specific value of $.$ In the tree for this problem, the $=2.$ Pruning is possible in nearly zero$-$sum games. Extend the alpha$-$beta pruning algorithm to this problem and specify the branches that will be pruned.

Find a general condition under which the children of a node $($S$)$ can be pruned in nearly zero$-$sum games. Your general condition should consider $U_A(S),U_B(S),$ and $.$