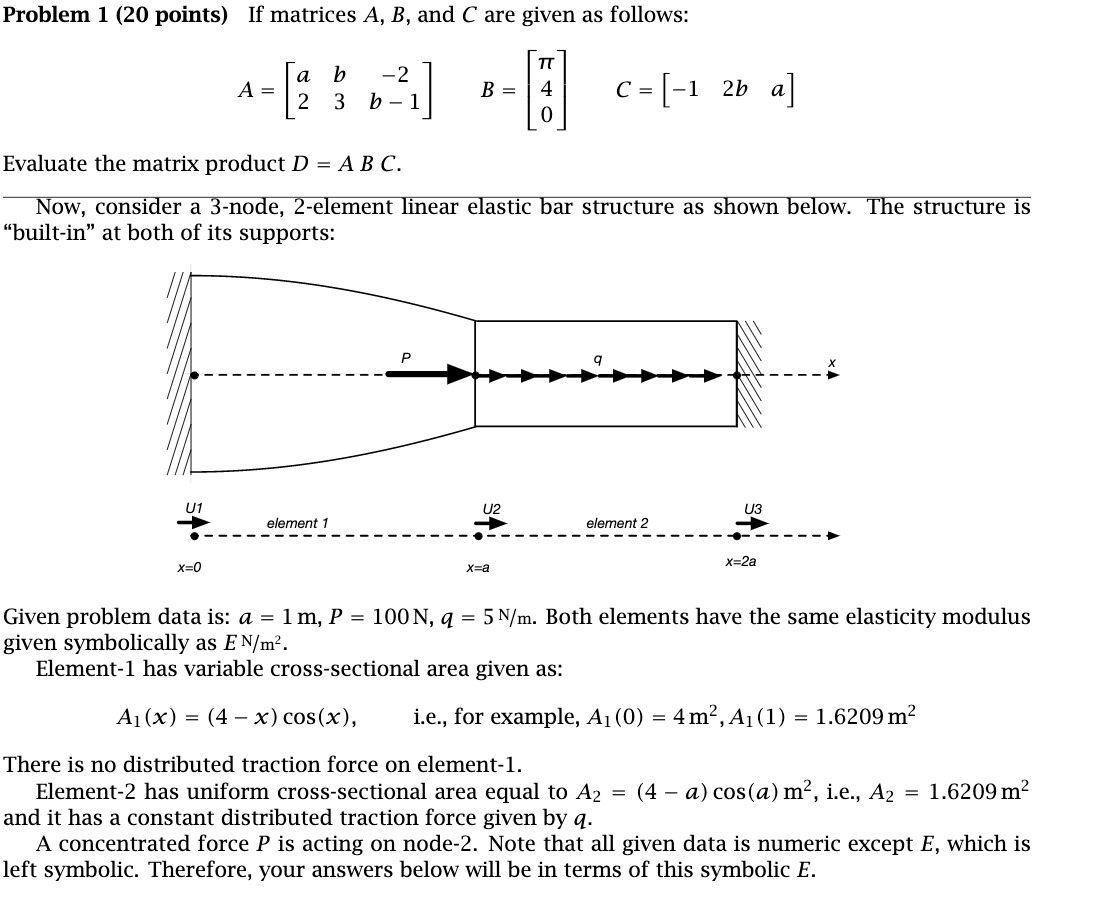
Problem 1 (20 points) If matrices A, B, and C are given as follows: 4 - | 2 36 B = C = -1 2b a] Evaluate the matrix product D = A B C. Now, consider a 3-node, 2-element linear elastic bar structure as shown below. The structure is "built-in" at both of its supports: U1 U2 U3 element 1 - - - - - element 2 - - - - - X=0 X=a x=2a Given problem data is: a = 1m, P = 100N, q = 5 N/m. Both elements have the same elasticity modulus given symbolically as EN/m2 Element-1 has variable cross-sectional area given as: Al (x) = (4 - x) cos(x), i.e., for example, Al (0) = 4m2, Al (1) = 1.6209m2 There is no distributed traction force on element-1. Element-2 has uniform cross-sectional area equal to A2 = (4 - a) cos(a) me, i.e., A2 = 1.6209m and it has a constant distributed traction force given by q. A concentrated force P is acting on node-2. Note that all given data is numeric except E, which is left symbolic. Therefore, your answers below will be in terms of this symbolic E