Question: Problem #1 (20 points total) Assume a $1,000 par value for the 2042 May 15, 3.00% coupon Treasury bond for the date February 25, 2021
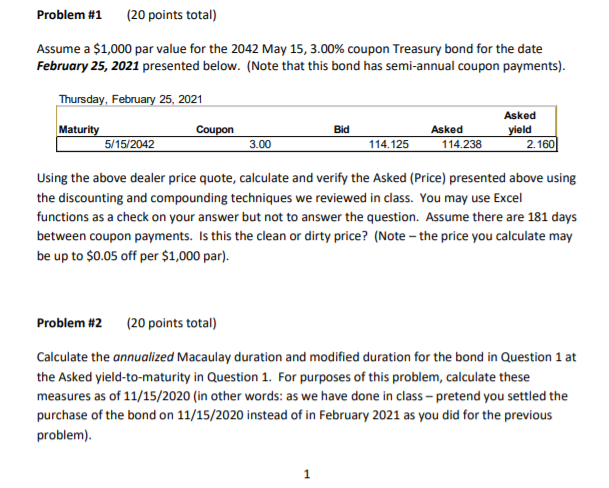

Problem #1 (20 points total) Assume a $1,000 par value for the 2042 May 15, 3.00% coupon Treasury bond for the date February 25, 2021 presented below. (Note that this bond has semi-annual coupon payments). Thursday, February 25, 2021 Maturity 5/15/2042 Coupon Bid Asked yield 2. 160 3.00 Asked 114.238 114.125 Using the above dealer price quote, calculate and verify the Asked (Price) presented above using the discounting and compounding techniques we reviewed in class. You may use Excel functions as a check on your answer but not to answer the question. Assume there are 181 days between coupon payments. Is this the clean or dirty price? (Note - the price you calculate may be up to $0.05 off per $1,000 par). Problem #2 (20 points total) Calculate the annualized Macaulay duration and modified duration for the bond in Question 1 at the Asked yield-to-maturity in Question 1. For purposes of this problem, calculate these measures as of 11/15/2020 (in other words: as we have done in class - pretend you settled the purchase of the bond on 11/15/2020 instead of in February 2021 as you did for the previous problem). 1 Problem #3 (20 points total) a.) Calculate and report the annualized convexity measure of the bond in Question 1 as of 11/15/2020. Again, pretend you settled the purchase of the bond on 11/15/2020 instead of in February 2021 as you did in Problem #1. b.) Using the duration approximation formula only what percentage change in the price of the bond would you expect if the yield decreases by 250 basis points? What type of risk does duration and convexity measure? Problem #4 (20 points total) Suppose East Bay Technology Co. just paid a dividend of $0.55 on its common stock. The market requires a return of 9.00% for stocks with similar risk. The company is expected to increase its dividend by a constant 7.00% per year. How much should the stock sell for today (t=0)? Calculate and present your answer in three ways: using the Time Value of Money (TVM) formula on a time line, the constant growth Present Value formula as well as the Net Present Value Excel function. Problem #5 (20 points total) Now suppose that instead of increasing it's divided by a constant 7.00% per year, East Bay Technology Co. will instead increase dividends by 7.00% for the first four years, by 4.75% for the following five years and after that increase dividends at a constant rate of only 2.00% per year indefinitely. How much should the stock sell for today (t=0)? Calculate and present your answer in three ways: using the Time Value of Money (TVM) formula on a time line, the variable-rate growth Present Value formula as well as the Net Present Value Excel function. Problem #1 (20 points total) Assume a $1,000 par value for the 2042 May 15, 3.00% coupon Treasury bond for the date February 25, 2021 presented below. (Note that this bond has semi-annual coupon payments). Thursday, February 25, 2021 Maturity 5/15/2042 Coupon Bid Asked yield 2. 160 3.00 Asked 114.238 114.125 Using the above dealer price quote, calculate and verify the Asked (Price) presented above using the discounting and compounding techniques we reviewed in class. You may use Excel functions as a check on your answer but not to answer the question. Assume there are 181 days between coupon payments. Is this the clean or dirty price? (Note - the price you calculate may be up to $0.05 off per $1,000 par). Problem #2 (20 points total) Calculate the annualized Macaulay duration and modified duration for the bond in Question 1 at the Asked yield-to-maturity in Question 1. For purposes of this problem, calculate these measures as of 11/15/2020 (in other words: as we have done in class - pretend you settled the purchase of the bond on 11/15/2020 instead of in February 2021 as you did for the previous problem). 1 Problem #3 (20 points total) a.) Calculate and report the annualized convexity measure of the bond in Question 1 as of 11/15/2020. Again, pretend you settled the purchase of the bond on 11/15/2020 instead of in February 2021 as you did in Problem #1. b.) Using the duration approximation formula only what percentage change in the price of the bond would you expect if the yield decreases by 250 basis points? What type of risk does duration and convexity measure? Problem #4 (20 points total) Suppose East Bay Technology Co. just paid a dividend of $0.55 on its common stock. The market requires a return of 9.00% for stocks with similar risk. The company is expected to increase its dividend by a constant 7.00% per year. How much should the stock sell for today (t=0)? Calculate and present your answer in three ways: using the Time Value of Money (TVM) formula on a time line, the constant growth Present Value formula as well as the Net Present Value Excel function. Problem #5 (20 points total) Now suppose that instead of increasing it's divided by a constant 7.00% per year, East Bay Technology Co. will instead increase dividends by 7.00% for the first four years, by 4.75% for the following five years and after that increase dividends at a constant rate of only 2.00% per year indefinitely. How much should the stock sell for today (t=0)? Calculate and present your answer in three ways: using the Time Value of Money (TVM) formula on a time line, the variable-rate growth Present Value formula as well as the Net Present Value Excel function
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


