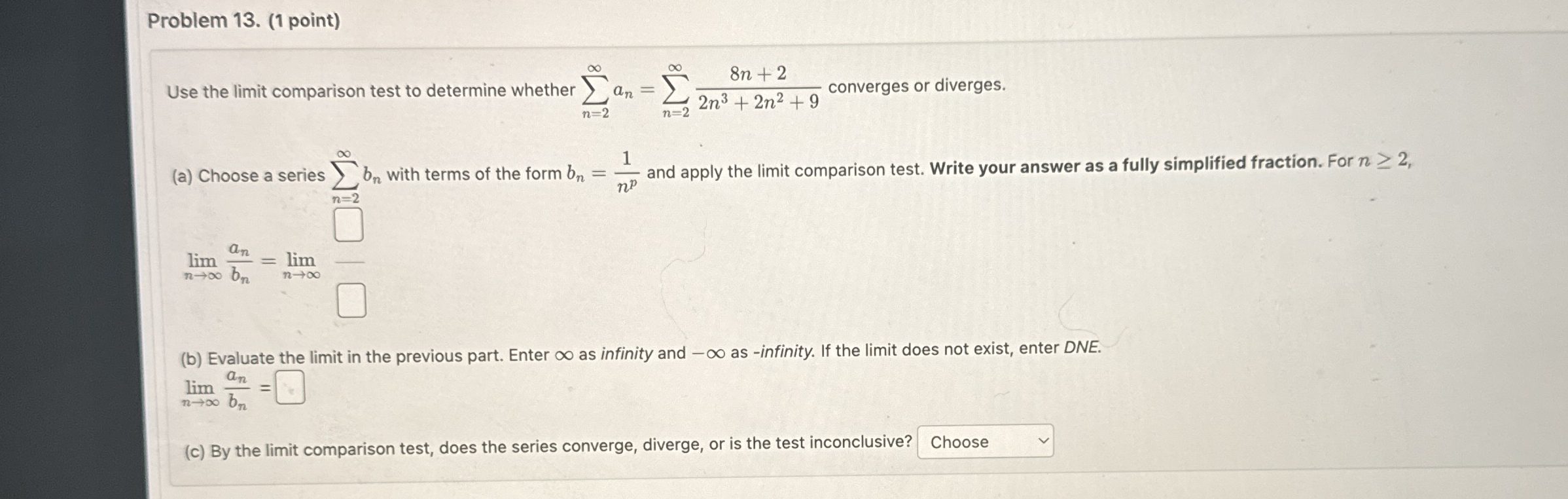
Problem $13.(1$ point$)$

Use the limit comparison test to determine whether ${\displaystyle \underset{n=2}{\overset{}{}}}{a}_n={\displaystyle \underset{n=2}{\overset{}{}}}\frac{8n+2}{2n^3+2n^2+9}$ converges or diverges.

$($a$)$ Choose a series ${\displaystyle \underset{n=2}{\overset{}{}}}{b}_n$ with terms of the form $b_n=\frac{1}{n^p}$ and apply the limit comparison test. Write your answer as a fully simplified fraction. For $n2,$

$\underset{n}{lim}\frac{a_n}{b_n}=\underset{n}{lim}$

$q,$

$$

$($b$)$ Evaluate the limit in the previous part. Enter $$ as infinity and $-$ as $-$infinity. If the limit does not exist, enter DNE.

$\underset{n}{lim}\frac{a_n}{b_n}=$

$($c$)$ By the limit comparison test, does the series converge, diverge, or is the test inconclusive?