Problem 1: (5 0 points) Given the network shown below, where the labels next to the nodes are the supplies/demand and the labels on the edges are the (costs, capacities) . We wish to minimize the cost of this transshipment problem.

a. Find a feasi ble spanning tree for this problem.

b. Given this spanning tree, use the network simplex algorithm to determine the dual prices for this spanning tree and the associated reduced costs of all non - basic arcs.

c. Is the spanning tree optimal? If not, indicate the e ntering arc, the leaving arc and how much flow would be increased/decreased on this arc and perform one pivot. If it is optimal, prove that it is by stating the optimality conditions, i.e., show that there are no violating non - basic arcs.

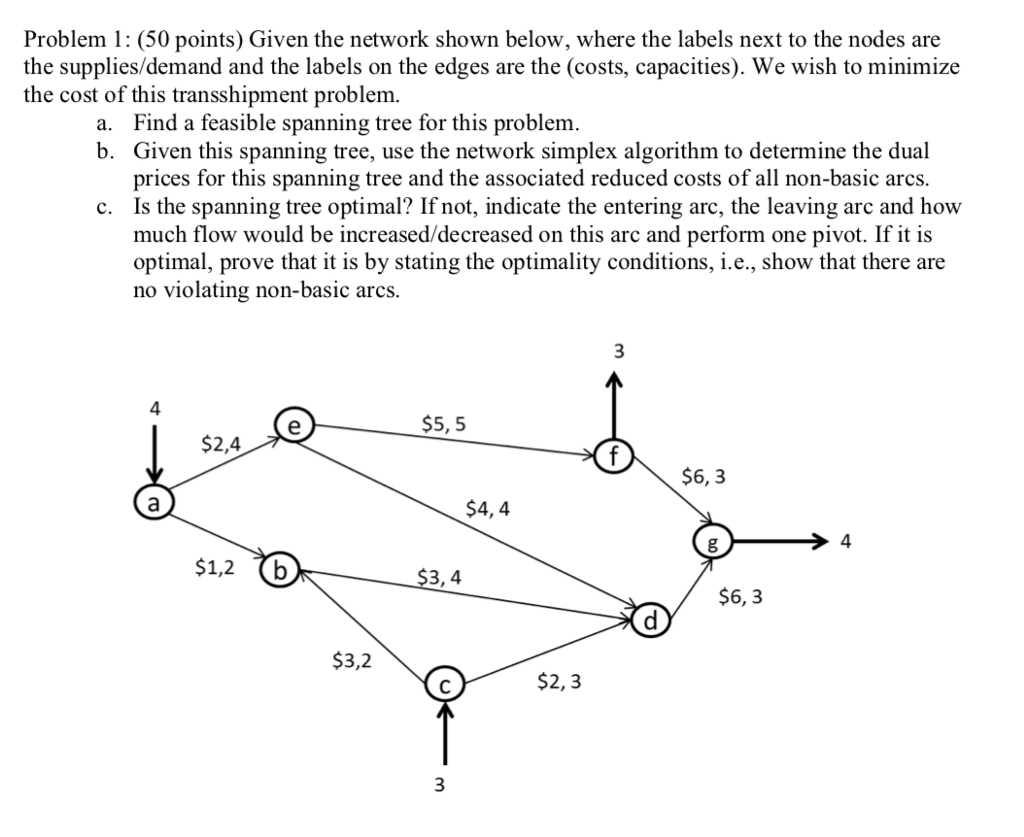
Problem 1: (50 points) Given the network shown below, where the labels next to the nodes are and and the labels on the edges are the (costs, capacities). We wish to minimize the cost of this transshipment problem. Find a feasible spanning tree for this problem. Given this spanning tree, use the network simplex algorithm to determine the dual prices for this spanning tree and the associated reduced costs of all non-basic arcs Is the spanning tree optimal? If not, indicate the entering arc, the leaving arc and how much flow would be increased/decreased on this arc and perform one pivot. If it is optimal, prove that it is by stating the optimality conditions, i.e., show that there are no violating non-basic arcs. a. b. c. 4 $5, 5 $2,4 $6,3 $4,4 4 12$3,4 $6, 3 $3,2 $2, 3 Problem 1: (50 points) Given the network shown below, where the labels next to the nodes are and and the labels on the edges are the (costs, capacities). We wish to minimize the cost of this transshipment problem. Find a feasible spanning tree for this problem. Given this spanning tree, use the network simplex algorithm to determine the dual prices for this spanning tree and the associated reduced costs of all non-basic arcs Is the spanning tree optimal? If not, indicate the entering arc, the leaving arc and how much flow would be increased/decreased on this arc and perform one pivot. If it is optimal, prove that it is by stating the optimality conditions, i.e., show that there are no violating non-basic arcs. a. b. c. 4 $5, 5 $2,4 $6,3 $4,4 4 12$3,4 $6, 3 $3,2 $2, 3