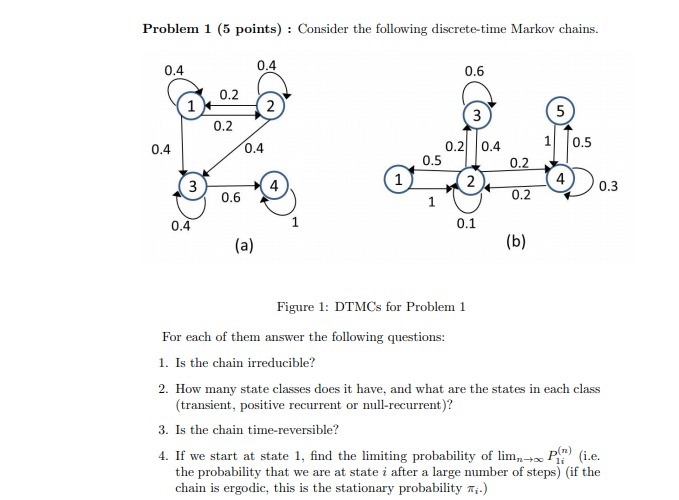
Question: Problem 1 (5 points) : Consider the following discrete-time Markov chains. 0.4 0.4 0.6 0.2 1 3 5 0.2 0.4 0.4 0.2 0.4 1 0.5
Problem 1 (5 points) : Consider the following discrete-time Markov chains. 0.4 0.4 0.6 0.2 1 3 5 0.2 0.4 0.4 0.2 0.4 1 0.5 0.5 0.2 3 1 2 0.3 0.6 1 0.2 0.4 0.1 (a) (b) Figure 1: DTMCs for Problem 1 For each of them answer the following questions: 1. Is the chain irreducible? 2. How many state classes does it have, and what are the states in each class (transient, positive recurrent or null-recurrent )? 3. Is the chain time-reversible? 4. If we start at state 1, find the limiting probability of lim, x P; (i.e. the probability that we are at state i after a large number of steps) (if the chain is ergodic, this is the stationary probability mi.)Problem 2 (5 points): Jobs arrive into a system consisting of two servers, according to a Poisson process with rate A jobs/sec. Job sizes are exponentially distributed. A job arriving is sent to server 1 with probability p, which can serve jobs with rate #1 jobs/sec. Otherwise, it is sent to server 2, which can serve jobs with rate /2 jobs/sec. Each server has its own queue, and can fit up to K total jobs (i.e. 1 in service and K, and A2 to ensure the system is stable? 2. What is the mean response time ET] for this system? 3. What is the mean response time for jobs of domain 1? 4. Consider the following modification to the system: 1 out of 2 jobs finishing from server 3 now go back to server 1 (instead of server 2). The rest exit the system, as before. Do you expect that E will increase, decrease, or stay the same? What about the mean response time for jobs of domain 1? (Note: It might not be necessary to redo all calculations. You just need to justify your answer shortly).Problem 4 (5 points): Consider a system of N unreliable servers. . A working server goes down with rate f = 1, independently of other servers. The time until it goes down is exponentially distributed. . A server which is down, gets repaired with rate r = 1, independently of other servers. The repair time is exponentially distributed. Answer the following questions: 1. What is the probability that all servers are down? 2. Assume N = 2 and that these servers are used in an M/M/2 system with Poisson (A) arrivals, and exp(p) distributed service times. Note however, that if a server is down, it stops serving jobs (until it gets repaired). Draw an appropriate CTMC for this system. 3. Assume now that if all servers are down at some point, then the system goes into a "batch repair" state. The batch repair time is exponentially distributed with rate N . r = N, but all servers are repaired together. Le., when it finishes all servers are back to working. Compared to question 2. is the mean response of this system faster, slower, or the same? Justify your