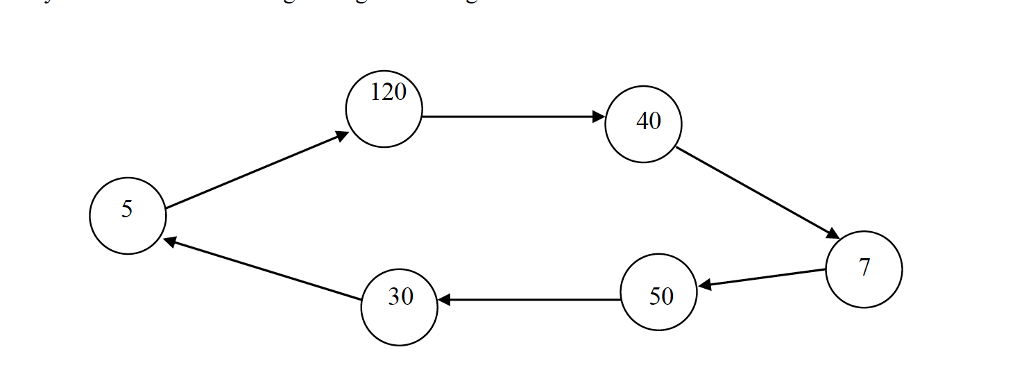Problem 1 (50 pts). Let G be an arbitrary set of n countries. Some of these countries have problems with one another. A set A of countries from G is perfect if no two of them have problems with one another. The problem MPP of finding a perfect set of countries with the maximal total weight is considered intractable although solvable in the general case. That is why a special case of G is considered. Assume that the structure of G is cyclic and find an efficient algorithm for solving MPP. An example of a cyclic structure with weights is given in Figure 1.

120 40 5 30 50