Question: Problem 1 . a . L : In - Xx 71 *, +3X, 2X1 - 72 Let B, = { [:] , 181, 1813

![71 *, +3X, 2X1 - 72 Let B, = { [:] ,](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/67064688d687a_52067064688c585b.jpg)

![, Let B, = "[:], 18], 1813 ( standard basis of U](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/67064689a7b67_521670646899451a.jpg)
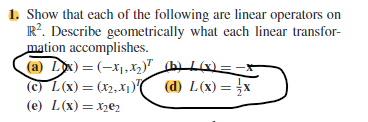
![B, to B2. Check that [ L ( X ) ] B,](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/6706468a4111f_5226706468a2f5f2.jpg)
Problem 1 . a . L : In " - Xx 71 *, +3X, 2X1 - 72 Let B, = { [:] , 181, 1813 ( standard basis of U = IR ) e, e , Let B, = "[:], 18], 1813 ( standard basis of U = /R ) e , Find the matrix representation of L from B, to B2. Check that [ L ( X ) ] B, = [L ]Be. X b. Let L: 12 2 - 19? be a rotation through the angle 8 : 17/ 4 . Let B, = [ ], [:]3 ( standard basis of U = 1R" ) Let B, = 3, [:13 ( standard basis of Y= /" ) e ,Find the matrix representation of L from B, to B2. Use this matrix to find L ( [ :, ] ) 3 C. L: IR - IR Let B, =[8 ]. [:]} e , Let B, =[: ]. . 1:15 Find the matrix representation of L from B, to B2. Use this matrix to find 2*2 J. L : P. IR Lla+by + (x" ) = [ 8 "a]Let B, = 1 1, x, x 2 7 En EX Find the matrix representation of L from B , to B2 . Use this matrix to find [ L (1- 2x + x2 ) ) 8, e. L : P, - Py Let B, = 2 1, x, x3 3 Let B2 = 1, x, x", x3 } Assume that [L 132 BI Find a formula for L ( a + 6x + cx ? ) ( Note that this should be a polynomial of degree lesser than 4 )1x2 f. L: Px IR Let B, = 1 1, x7 Let B, : }[: : ]. [: ]. [. : ]. 18 0]] EN Ey Assume that the matrix representation of I from B, to BE is O D O Find a formula for 1 ( a + bx ) ( Note that this should be a 2 x2 matrix )1. Show that each of the following are linear operators on IR . Describe geometrically what each linear transfor- mation accomplishes. (c) L(x) = (12.XD)( (d L(X) = NI- X (e) L (x) = X202Determine whether the following are linear transforma- tions from P2 to P3: (@) L(p(x)) =xp(x) (b) Loom)) =r (@ L(p(x)) = p(x) + xp(x)+xp'(x)
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


