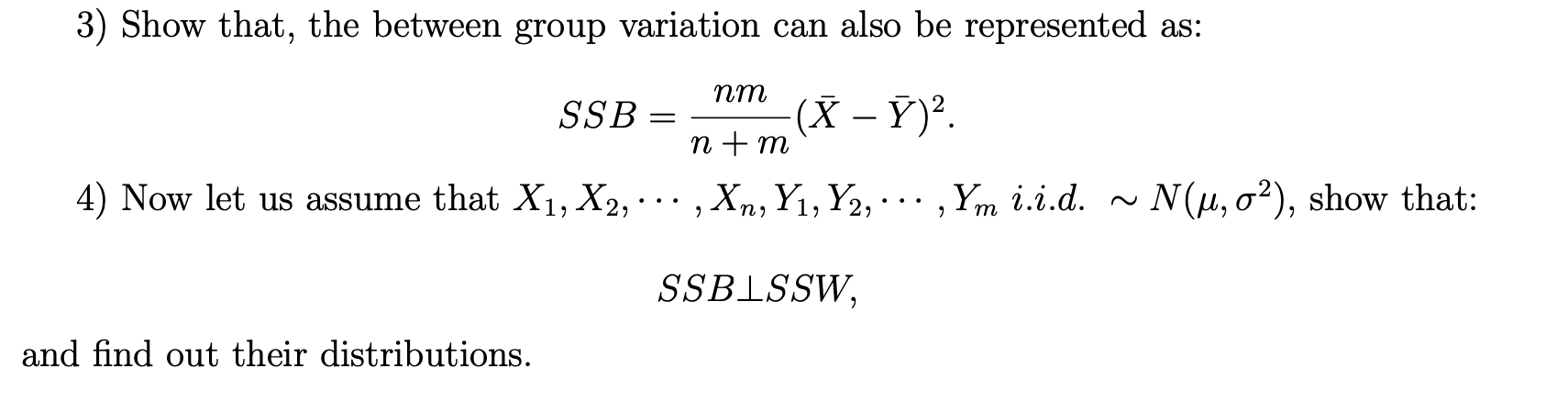
Problem 1. (Analysis of Variance) Let X1, X2, . .. Xn be random sample with finite mean /x and variance or, and Y1, Y2, . . . Ym be another random sample with finite mean My and variance o2. Assuming that X1, X2, . . . , Xn, Yl, Y2, . .. , Ym are fully independent and use X and S'Y to represent the sample mean and sample variance for Xis as X and S3, Y and Sy to represent the sample mean and sample variance for Yis . Answer the following questions. 1) Define the grand mean as: K = Ell Xi+ EMY; n t m Show that, K = (nX + my)/(n + m).3) Show that, the between group variation can also be represented as: SSB = nm n + m ( X - Y ) 2. 4) Now let us assume that X1, X2, . . . , Xn, Yl, Y2, . .. , Ym i.i.d. ~ N(M, 02), show that: SSBLSSW, and find out their distributions