Problem 1 : Apply Johnsons rule to develop a schedule for the following 2-machine serial systems. Can you prove that your schedule is exactly optimal, why or why not?

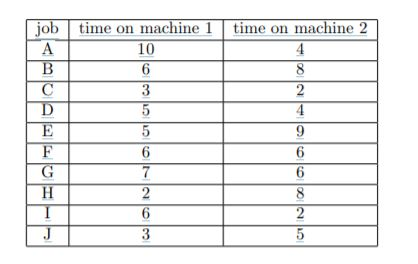
Problem 2 : Suppose that you are managing a security check point where entrants first have their documents reviewed and then go through luggage inspection. A group of seven entrants just arrived. You are free to choose which ones of them to process earlier. Your want to complete the admission of the entire group as quickly as possible. The estimated processing times are given as follows:

Question:

1. (6 points) Develop a schedule of processing these entrants, and explain why your schedule takes the shortest amount of time to get them through.

2. (4 points) After checking the first entrant, the luggage inspector was paged by a nearby Panera that her lunch is ready. She wants to take a 3-minute break to get it sometime between now and before the entire group has been admitted. Can she do that without delaying the group? Why?

3. (4 points) The document reviewer was also paged by another place, and asked if he can take a 2-minute break to get his lunch. Given that you do not want any delay, would you let him go before he finishes the entire group? Why?

4. (4 points) Do you want to change your answer to question 3 if someone brought additional luggage to entrant E, which increases his luggage inspection time to 18?

Problem 3 (16 points): You are competing for a contract in a second-price auction. The cost for you to fulfill the contract is $10m. Check if each of the following statements is true. If not, change the statement to make it correct.

1. (4 points) If with probability 0.4, the lowest cost of your competitors is $6m and with probability 0.6, it is $15m. Then your expected profit from the auction is $1.4m.

2. (4 points) If one of your competitors can fulfill the contract at cost $7m, then you are going to lose at least $3m.

3. (4 points) If 30% of chance that one of your competitors has a cost below $6m, 30% of chance that all of them have a cost above $16m, and 40% of chance all of them have a cost somewhere between $8m and $11m. Then your expected profit is at least $1.8m.

4. (4 points) If all your competitors inflate their ask prices above their costs by 10%, then you will be worse if you do not do so.

Problem 4 (6 points): Your company is invited to participate in a secondprice auction to compete for a contract. All participants are required to pay a entrance fee of x. The cost for you to fulfill the contract is $5m. You have a probability estimate of the lowest cost of your competitors, which is $3m with probability 0.3, $6m with probability 0.3, and $10m with probability 0.4. Your objective is to maximize the expected payoff. What is the maximum entrance fee (x) you should be willing to pay to participate?

in time on machine 1 time on machine 2 - - =E job person TABCDEFG document review time 14364 luggage inspection time 34 12 8