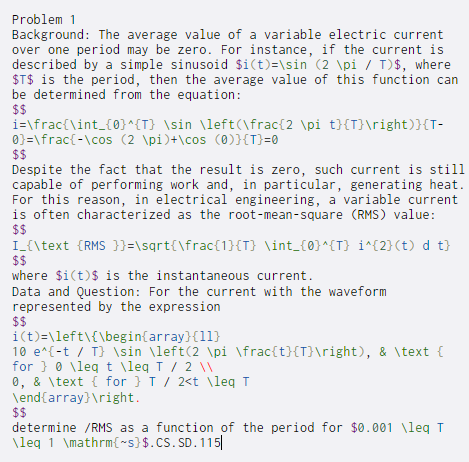
Problem 1 Background: The average value of a variable electric current over one period may be zero. For instance, if the current is described by a simple sinusoid $i(t)=\sin (2 \pi / D) $, where $T$ is the period, then the average value of this function can be determined from the equation: $$ i=\frac{\int_{0}^{T} \sin \left(\frac{ \pi t}{T} ight)}{T- 0}=\frac{-\cos (2 \pi +\cos }{T}=0 $$ Despite the fact that the result is zero, such current is still capable of performing work and, in particular, generating heat. For this reason, in electrical engineering, a variable current is often characterized as the root-mean-square (RMS) value: $$ I_{\text {RMS }}=\sqrt{\frac{1}{T} \int_{0}^{T} i^{2}(t) d t} $$ where $i(t)$ is the instantaneous current. Data and Question: For the current with the waveform represented by the expression $$ i(t)=\left\{\begin{array}{11} 10 e^{-t / T} \sin \left(2 \pi \frac{t}{T} ight), & \text { for } o\leq t \leq 1 / 2 0,& \text { for } 1 / 2