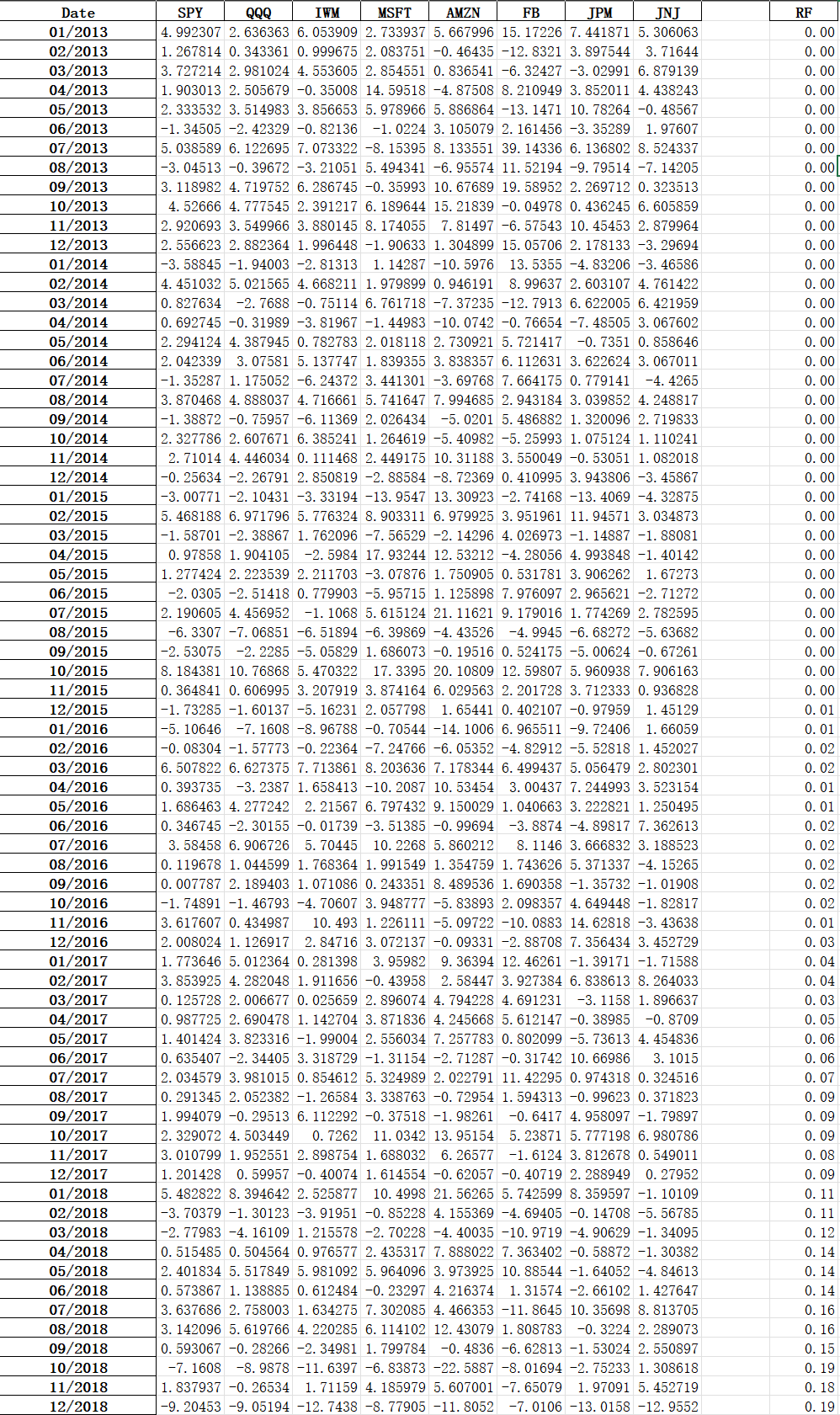
Problem 1: Calculate the expected annualized return and annualized standard deviation of the three stocks you've picked and for one of the indices (\$SPY for S\&P 500, \$QQQ for Nasdaq, or \$IWM for Russell 1000). Compute the Sharpe Ratio for each stock and one of the indices. Which of them delivers the highest Sharpe ratio? Discuss your results. Instead of evaluating the portfolio based on the end of the year average and standard deviation, we can also track the performance of the portfolio every month. The return of the portfolio in any given month is the weighted sum of the individual returns, rp=w1r1+w2r2+w3r3, of the stocks in that month. Create a new column in Excel which tracks the returns of your portfolio accordingly. a) Calculate the expected return, standard deviation, and Sharpe Ratio of the portfolio from this column of monthly returns. b) Compare your results with those from Problem 2. Explain any differences. Form a portfolio out of the three stocks. Assign weights w1,w2,w3 to each of them such that they sum up as w1+w2+w3=1, that means to 100%. a) Assume that the stocks are uncorrelated. Then the expected return is the weighted sum of the individual returns, E(rp)=w1E(r1)+w2E(r2)+w3E(r3), and the standard deviation is calculated according to p=w1212+w2222+w3232. Calculate the expected return and standard deviation of your portfolio. b) Compute the Sharpe Ratio for your portfolio. Does your portfolio offer an improvement over the individual stocks? Problem 1: Calculate the expected annualized return and annualized standard deviation of the three stocks you've picked and for one of the indices (\$SPY for S\&P 500, \$QQQ for Nasdaq, or \$IWM for Russell 1000). Compute the Sharpe Ratio for each stock and one of the indices. Which of them delivers the highest Sharpe ratio? Discuss your results. Instead of evaluating the portfolio based on the end of the year average and standard deviation, we can also track the performance of the portfolio every month. The return of the portfolio in any given month is the weighted sum of the individual returns, rp=w1r1+w2r2+w3r3, of the stocks in that month. Create a new column in Excel which tracks the returns of your portfolio accordingly. a) Calculate the expected return, standard deviation, and Sharpe Ratio of the portfolio from this column of monthly returns. b) Compare your results with those from Problem 2. Explain any differences. Form a portfolio out of the three stocks. Assign weights w1,w2,w3 to each of them such that they sum up as w1+w2+w3=1, that means to 100%. a) Assume that the stocks are uncorrelated. Then the expected return is the weighted sum of the individual returns, E(rp)=w1E(r1)+w2E(r2)+w3E(r3), and the standard deviation is calculated according to p=w1212+w2222+w3232. Calculate the expected return and standard deviation of your portfolio. b) Compute the Sharpe Ratio for your portfolio. Does your portfolio offer an improvement over the individual stocks