PROBLEM $1$: Cohesion, Bridges, and Local Bridges $(20\%)$

One of the goals in network science is to quantitatively describe the structure of a network.

On the global $($macroscopic$)$ level we can measure the connectedness of a network: num$-$

ber of connected components and their sizes. Let's now look into how connected those

connected component are. This is sometimes referred to as network cohesion. A cohesive

network$/$component is difficult to separate. Let's define network$/$component cohesion as

the minimal number of edges ${?}^1$ that need to be removed to disconnect the component.

An edge that if removed makes the network$/$component disconnected is called a bridge.

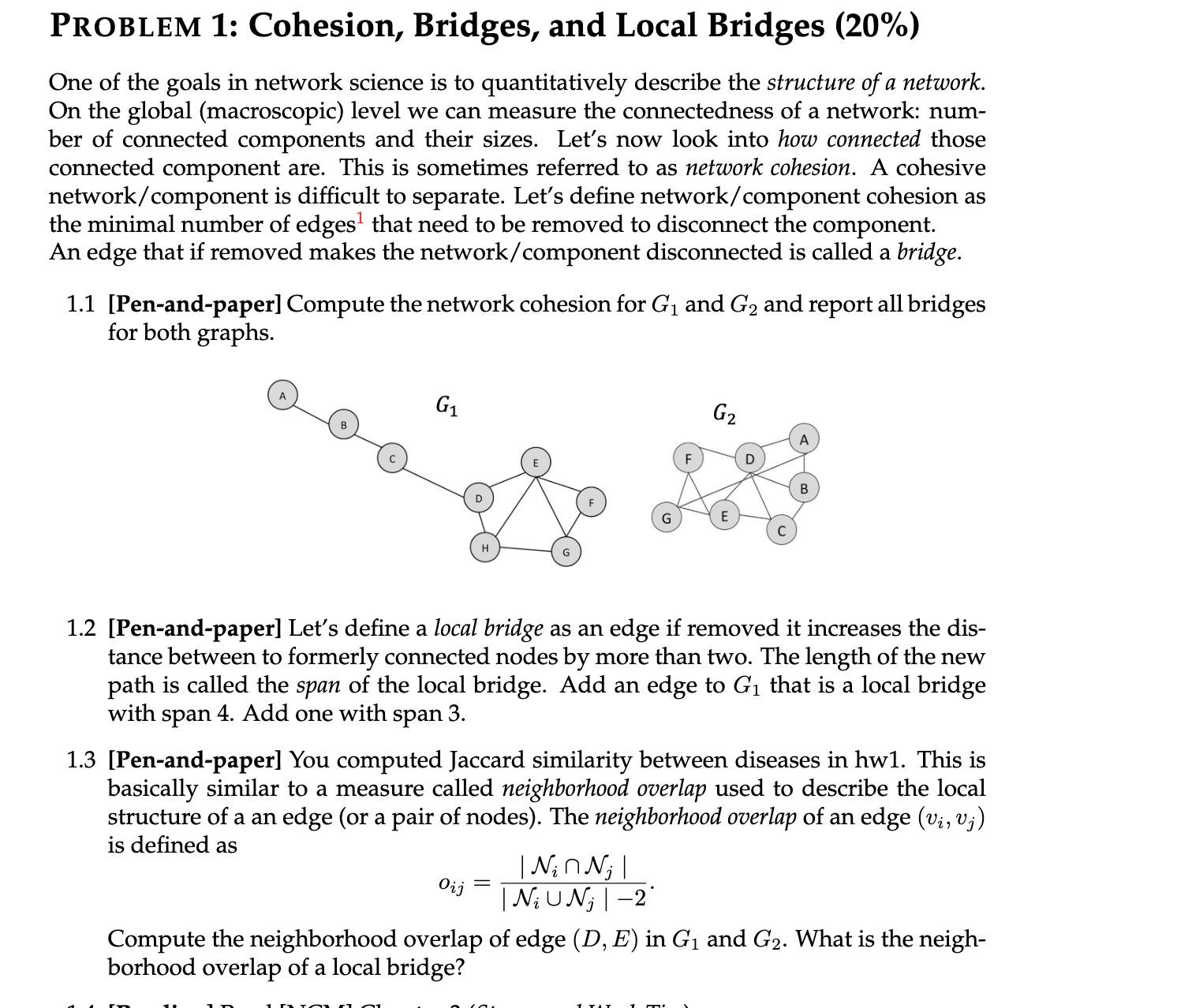
$1\mathrm{.}1[$Pen$-$and$-$paper$]$ Compute the network cohesion for $G_1$ and $G_2$ and report all bridges

for both graphs.

$1\mathrm{.}2[$Pen$-$and$-$paper$]$ Let's define a local bridge as an edge if removed it increases the dis$-$

tance between to formerly connected nodes by more than two. The length of the new

path is called the span of the local bridge. Add an edge to $G_1$ that is a local bridge

with span $4.$ Add one with span $3.$

$1\mathrm{.}3[$Pen$-$and$-$paper$]$ You computed Jaccard similarity between diseases in hw$1.$ This is

basically similar to a measure called neighborhood overlap used to describe the local

structure of a an edge $($or a pair of nodes$).$ The neighborhood overlap of an edge $(v_i,v_j)$

is defined as

$o_{ij}=\frac{|N_i{N}_j|}{|N_i{N}_j|-2}$

Compute the neighborhood overlap of edge $(D,E)$ in $G_1$ and $G_2.$ What is the neigh$-$

borhood overlap of a local bridge?