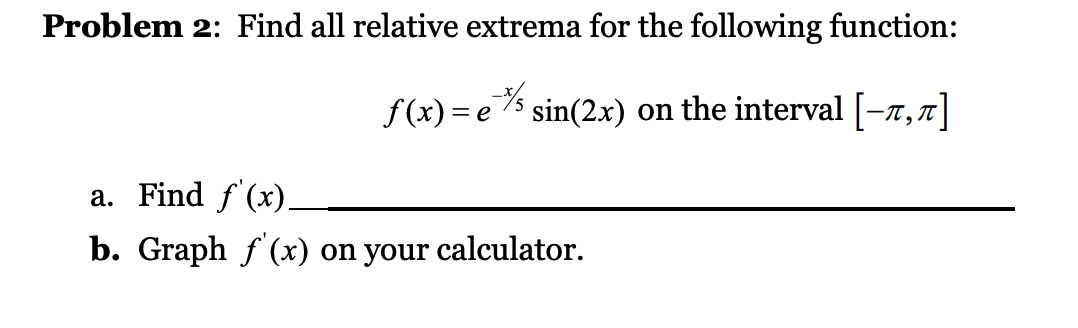
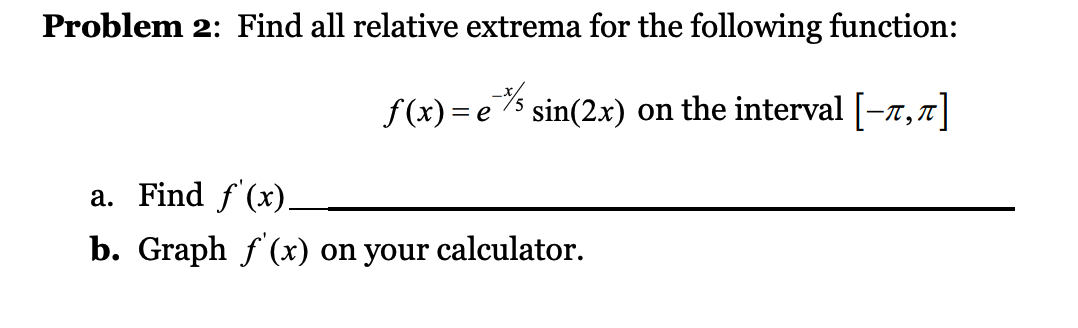
Problem 1: Find all relative extrema for the following function: f(x) =x-3x'+x+3x-66 a. Find f (x) b. Graph f (x) on your calculator. c. The zeros for f (x) are located at x =? d. f'(x) is undefined at x =?e. The critical numbers for f (x) are located at: || || 31 | f. The critical values for f (x) are: f(x1) : f(x2) : f(x3) : g. Graph both the function f (x) and its derivative f '(x) on the same set of axes. You should be able to see the extrema of the function line up with the critical numbers and critical values found above. h. The extrema at x1 is a relative max or a relative min? i. The extrema at 3:2 is a relative max or a relative min? J. The extrema at x3 is a relative max or a relative min? k. The domain and range for f (x) are: Domain: Range: 1. Turn in a sketch of the graph of both f (x) and f '(x) on the same axes. Problem 2: Find all relative extrema for the following function: f (x) = (5% sin(2x) on the interval [7r, 7:] a. Find f '(x) 1). Graph f '(x) on your calculator. The zeros for f '(x) are located at x : ? d. f '(x) is undened at x : ? e. The critical numbers for f (x) are located at: 5' x1 x2: x 9-1 x4: f. The critical values for f (x) are: f(x1) = f(x2) = f(x3) = f(x4) = The value of f (x) at the left endpoint is? f(a) = ? . The value of f (x) at the right endpoint is? f (b) = ? The maximum of f (x) on the interval is? was 0 H. I . The minimum of f (x) on the interval is? J k. Graph both the function f (x) and its derivative f '(x) on the same set of axes. You should be able to see the extrema of the function line up with the critical numbers and critical values found above. 1. The domain and rage for f (x) are: Domain: Range: m. Turn in a sketch of the graph of both f (x) and f '(x) on the same axes. Problem 3: Find the open intervals on which the function is increasing, decreasing or constant. 2x f ( x) = x2 - x+1 on (-3,3) a. Find f'(x) b. Graph f'(x) on your calculator. c. The zeros for f'(x) are located at x =? d. f'(x) is undefined at x =? e. The critical numbers for f(x) are located at: * = ? X, = ? f. The critical values for f (x) are: f (x, ) = ? f (x2 ) = ? g. Partition the number line into intervals using the procedure discussed above.h. f (x) is increasing on which intervals? i. f (x) is decreasing on which intervals? j. f (x) has a relative maximum(s) at what value(s) of x? Math 140 Lab Name: k. f (x) has a relative minimum(s) at what value(s) of x? 1. Turn in a sketch of the graph of both f (x) and f '(x) on the same axes