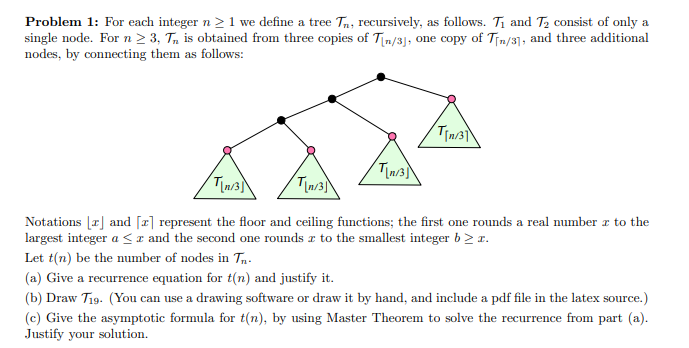
Problem 1: For each integer n> 1 we define a tree Tn, recursively, as follows. T1 and T2 consist of only a single node. For n 3, T, is obtained from three copies of Tin/3), one copy of Tin/31, and three additional nodes, by connecting them as follows: Tinal Th3 T11/3) Th30) Notations (2) and (2) represent the floor and ceiling functions; the first one rounds a real number x to the largest integer a I. Let t(n) be the number of nodes in T. (a) Give a recurrence equation for t(n) and justify it. (b) Draw T19. (You can use a drawing software or draw it by hand, and include a pdf file in the latex source.) (c) Give the asymptotic formula for t(n), by using Master Theorem to solve the recurrence from part (a). Justify your solution