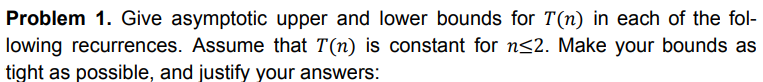
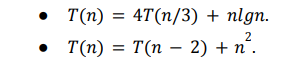
Problem 1. Give asymptotic upper and lower bounds for T(n) in each of the following recurrences. Assume that T(n) is constant for n2. Make your bounds as tight as possible, and justify your answers: T(n)=4T(n/3)+nlgnT(n)=T(n2)+n2 Problem 2. Can the master method be applied to the recurrence T(n)=4T(n/2)+n2lgn ? Why or why not? Give an asymptotic upper bound for this recurrence. Problem 3. Use a recursion tree to determine a good asymptotic upper bound on the recurrence T(n)=3T(n/2)+n. Use the substitution method to verify your