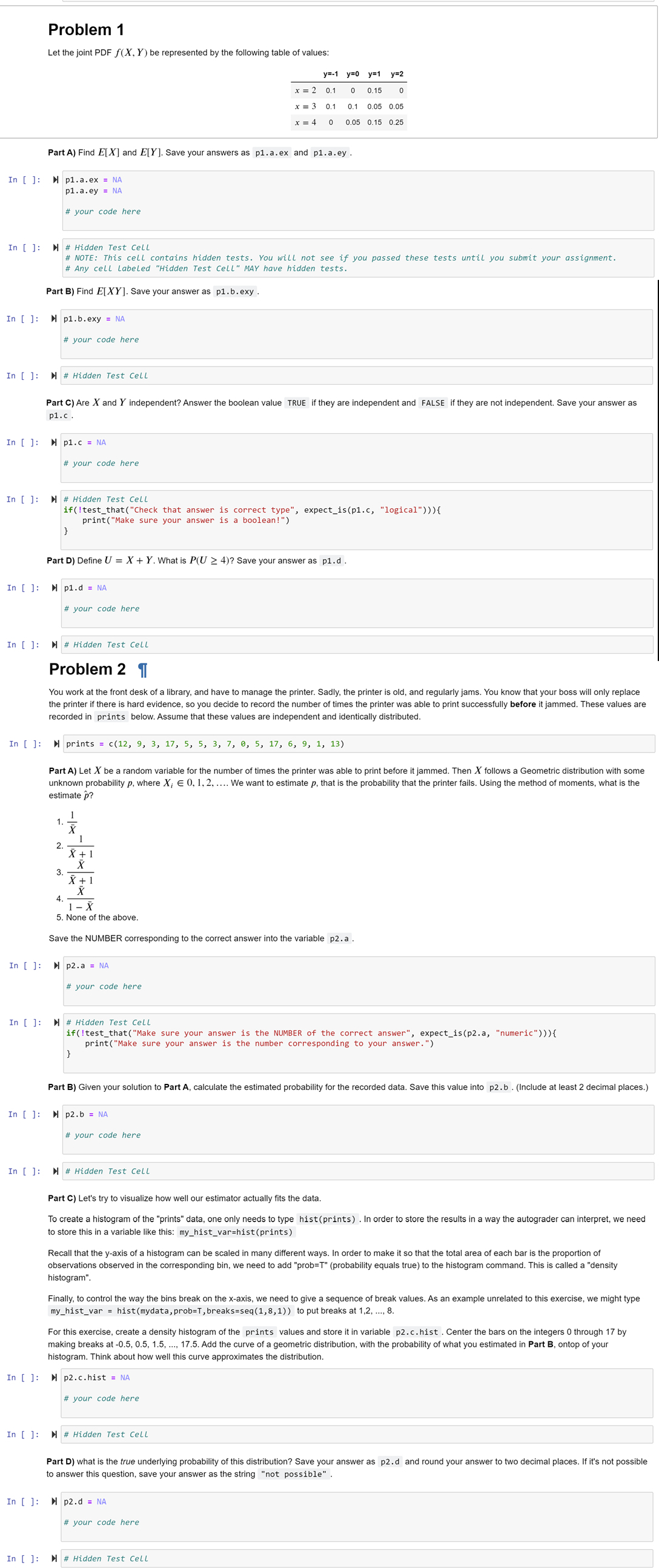
Problem $1$

Let the joint PDF $f(x,Y)$ be represented by the following table of values:

$,y=-1,y=0,y=1,y=2$

$x=2,0\mathrm{.}1,0,0\mathrm{.}15,0$

$x=3,0\mathrm{.}1,0\mathrm{.}1,0\mathrm{.}05,0\mathrm{.}05$

$x=4,0,0\mathrm{.}05,0\mathrm{.}15,0\mathrm{.}25$

Part A$)$ Find $E[x]$ and $E[Y].$ Save your answers as p$1.$a$.$ex and p$1.$a$.$ey $.$

In $[]$: $p1.a.ex=NA$

$p1.a.ey=NA$

# your code here

# Hidden Test Cell

# NOTE: This cell contains hidden tests. You will not see if you passed these tests until you submit your assignment.

# Any cell labeled "Hidden Test Cell" MaY have hidden tests.

Part B$)$ Find $E[xY].$ Save your answer as p$1.$b$.$exy $.$

v p$1.$b$.$exy $=$ NA

# your code here

In $[]$: # Hidden Test Cell

Part C$)$ Are $x$ and $Y$ independent? Answer the boolean value TRUE if they are independent and FALSE if they are not independent. Save your answer as

p$1.$c$.$

p$1.$c $=$ NA

# your code here

# Hidden Test Cell

if$(!$test$\_$that$("$Check that answer is correct type", expect$\_$is$($p$1.$c$,$ "logical"$)))\{$ print$("$Make sure your answer is a boolean!"$)$

Part D$)$ Define $U=x+Y.$ What is $P(U4)?$ Save your answer as p$1.$d

$p1*d=NA$

# your code here

$$ # Hidden Test Cell

Problem $2$ I$$

You work at the front desk of a library, and have to manage the printer. Sadly, the printer is old, and regularly jams. You know that your boss will only replace

the printer if there is hard evidence, so you decide to record the number of times the printer was able to print successfully before it jammed. These values are

recorded in prints below. Assume that these values are independent and identically distributed.

prints $=c(12,9,3,17,5,5,3,7,0,5,17,6,9,1,13)$

Part A$)$ Let $x$ be a random variable for the number of times the printer was able to print before it jammed. Then $x$ follows a Geometric distribution with some

unknown probability $p,$ where $x_{i}in0,1,2,$dots. We want to estimate $p,$ that is the probability that the printer fails. Using the method of moments, what is the

estimate hat$(p)?$

$\frac{1}{(\stackrel{}{x})}$

$\frac{1}{(\stackrel{}{x})+1}$

$\frac{(\stackrel{}{x})}{(\stackrel{}{x})+1}$

$\frac{(\stackrel{}{x})}{1-(\stackrel{}{x})}$

None of the above.

Save the NUMBER corresponding to the correct answer into the variable p$2.$a

if$(!$test$\_$that$("$Make sure your answer is the NUMBER of the correct answer", expect$\_$is$($p$2.$a$,$ "numeric"$)))\{$

print$("$Make sure your answer is the number corresponding to your answer."$)$

Part B$)$ Given your solution to Part A$,$ calculate the estimated probability for the recorded data. Save this value into p$2.$b $.($Include at least $2$ decimal places.$)$

Part C$)$ Let's try to visualize how well our estimator actually fits the data.

To create a histogram of the "prints" data, one only needs to type hist $($prints$).$ In order to store the results in a way the autograder can interpret, we need

to store this in a variable like this: my$\_$hist$\_$var$=$hist $($prints$)$

Recall that the $y-$axis of a histogram can be scaled in many different ways. In order to make it so that the total area of each bar is the proportion of

observations observed in the corresponding bin, we need to add "prob$=$T$"($probability equals true$)$ to the histogram command. This is called a "density

histogram".

Finally, to control the way the bins break on the $x-$axis, we need to give a sequence of break values. As an example unrelated to this exercise, we might type

my$\_$hist$\_$var $=$ hist $($mydata$,$ prob $=T,$ breaks $=$seq$(1,8,1))$ to put breaks at $1,2,$dots,$8.$

For this exercise, create a density histogram of the prints values and store it in variable p$2.$c$.$ hist $.$ Center the bars on the integers $0$ through $17$ by

making breaks at $-0\mathrm{.}5,0\mathrm{.}5,1\mathrm{.}5,$dots,$17\mathrm{.}5.$ Add the curve of a geometric distribution, with the probability of what you estimated in Part B$,$ ontop of your

histogram. Think about how well this curve approximates the distribution.

In $[]$: p$2.$c$.$hist $=$ NA

# your code here

In $[]$: # Hidden Test cell

Part D$)$ what is the true underlying probability of this distribution? Save your answer as p$2.$d and round your answer to two decimal places. If it's not possible

to answer this question, save your answer as the string "not possible"