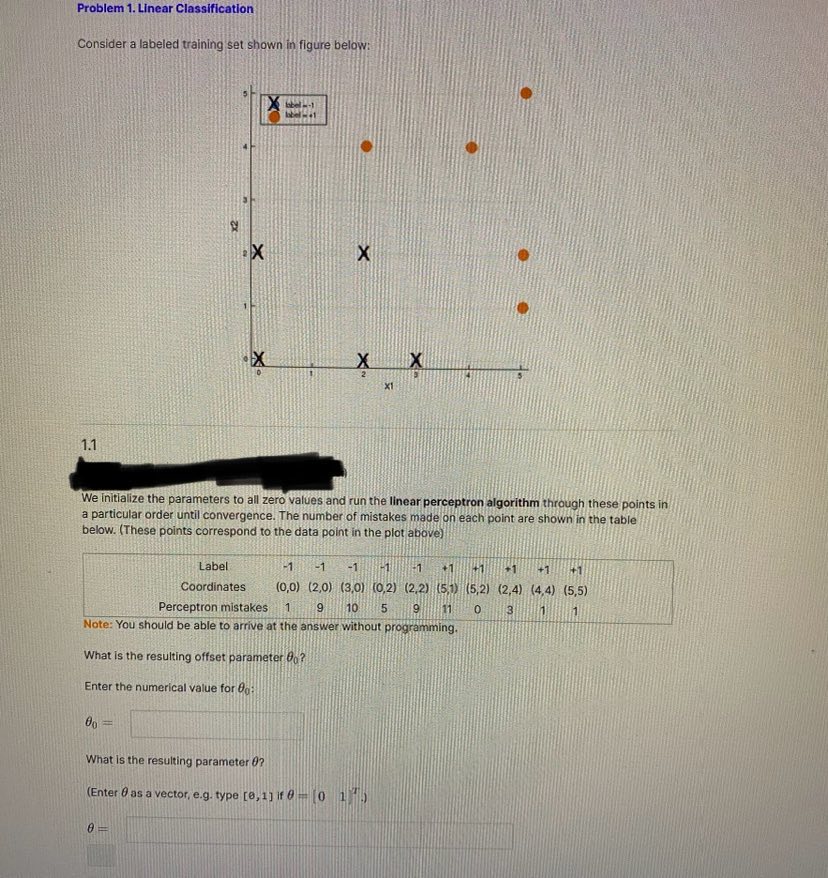
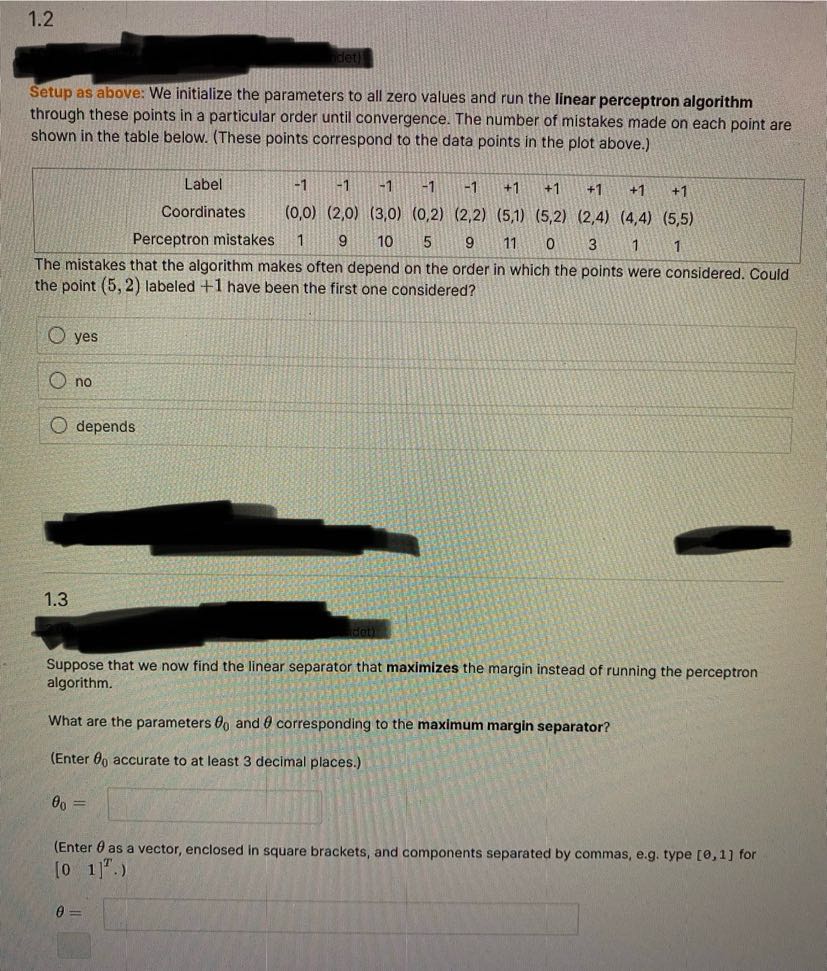
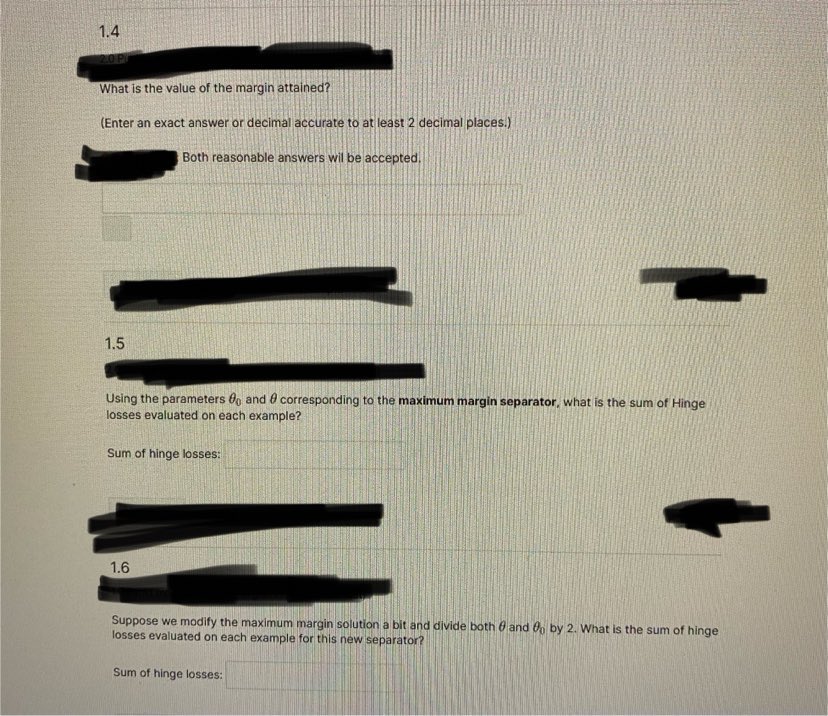
Problem 1. Linear Classification Consider a labeled training set shown in figure below: X X X X X 1.1 We Initialize the parameters to all zero values and run the linear perceptron algorithm through these points in a particular order until convergence. The number of mistakes made on each point are shown in the table below. (These points correspond to the data point in the plot above) Label -1 -1 -1 -1 1 +1 -1 +1 +1 Coordinates (0,0) (2,0) (3,0) (0,2) (2,2) (5,1) (5,2) (2,4) (4,4) (5,5) Perceptron mistakes 1 9 10 5 9 11 0 3 Note: You should be able to arrive at the answer without programming. What is the resulting offset parameter On? Enter the numerical value for do: What Is the resulting parameter 0? (Enter O as a vector, e.g. type [e, 1] if 0 - [0 1 5)1.2 Setup as above: We initialize the parameters to all zero values and run the linear perceptron algorithm through these points in a particular order until convergence. The number of mistakes made on each point are shown in the table below. (These points correspond to the data points in the plot above.) Label 1-1 -1 -1 -1 +1 +1 +1 +1 +1 Coordinates (0,0) (2,0) (3,0) (0,2) (2,2) (5,1) (5,2) (2,4) (4,4) (5,5) Perceptron mistakes 1 9 10 5 9 11 3 The mistakes that the algorithm makes often depend on the order in which the points were considered. Could the point (5, 2) labeled + 1 have been the first one considered? yes O no depends 1.3 Suppose that we now find the linear separator that maximizes the margin instead of running the perceptron algorithm. What are the parameters 0 and @ corresponding to the maximum margin separator? (Enter do accurate to at least 3 decimal places.) 60 = (Enter 0 as a vector, enclosed in square brackets, and components separated by commas, e.g. type [0, 1] for [0 1]".) 0 =1.4 What is the value of the margin attained? (Enter an exact answer or decimal accurate to at least 2 decimal places.) Both reasonable answers wil be accepted 1.5 Using the parameters 0 and / corresponding to the maximum margin separator, what is the sum of Hinge losses evaluated on each example? Sum of hinge losses: 1.6 Suppose we modify the maximum margin solution a bit and divide both 0 and do by 2. What is the sum of hinge losses evaluated on each example for this new separator? Sum of hinge losses