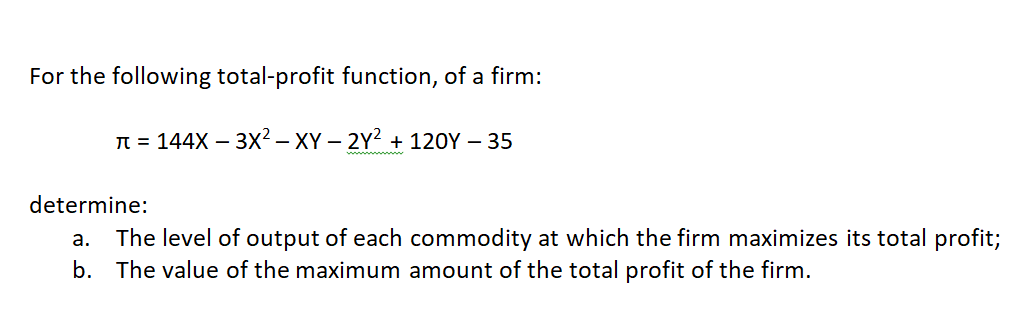
Problem 1 (Partial Derivatives)

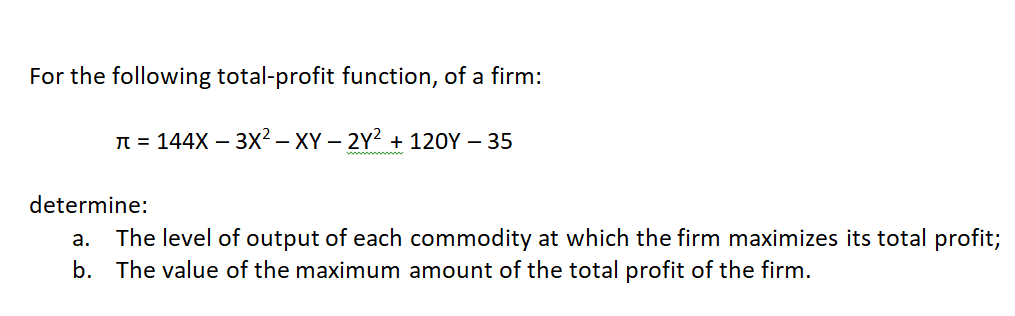
Year Y X 1 18.00 1.40 2 18.50 1.90 3 12.00 2.00 4 14.00 2.30 5 15.00 1.90 6 12.00 2.40 2' 15.60 2.90 8 14.00 3.00 9 13.00 3.50 10 13.50 3.10 Y = Average ton yield of rice in one hectare of land )1 = Average Carbon Dioxide level (in kilograms per cubic meter) in the atmosphere (Indicator of Climate Change) Answer this: Does the average level of climate change influences the average veild of rice per hectare? 1. Linear Programming Problem It takes 3 hours of labor, 5 kgs of wood, and 1 kg of metal to build a furniture. To make a doghouse, it takes 4 hours of labor, 6 kgs of wood and 2 kg of metal, while to make a wooden utensil, it takes 1 hour of labor, 0.5 kg of wood and 0.1 kg. of metal. Available labor per month is 12,000 hours, available wood is 1000 kilograms, and metal is 900 kgs. Profit from furniture is 200 pesos, doghouse is 500 pesos and for utensil, its 20 pesos. Demand for furniture per month is 200, doghouse is 150 and utensils is 300. What should be the units produced each of furniture, doghouse and wooden utensils to maximize profits without exceeding demand and available resources? Show the solution matrix, objective function, constraints, of course the optimal number of furniture, doghouse & wooden utensils and the maximum profit possible. 2. Derivative Problem A hypothetical airline company has its plane ticket sales function hereunder: Y = 87X--32.1X +5 a. Find the first derivative. b. Find the value of Y in the sales function upon finding the value of X in the first derivative. c. Is the derived Y (ticket sales) a minimum or a maximum? Why?For the following total-profit function, of a firm: TI: = 144x 3X2 XY 2Y2 + 120Y 35 determine: a. The level of output of each commodity at which the firm maximizes its total profit; b. The value of the maximum amount ofthe total profit of the firm