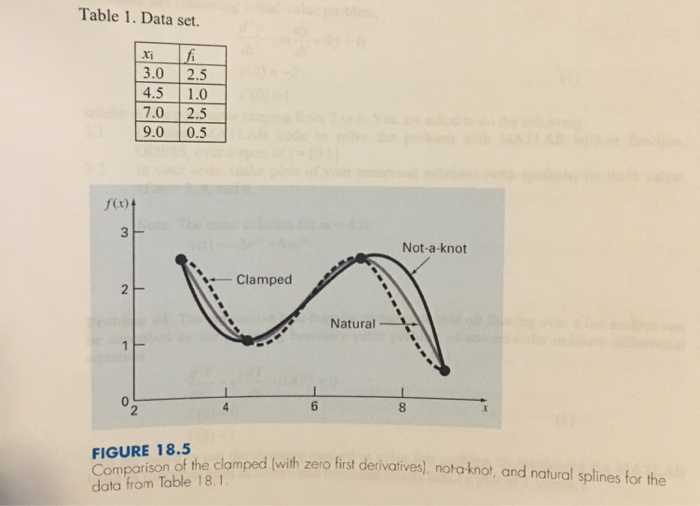
?

Problem #1. The cubic splines employ a third-order polynomial function, s(x), for each interval between knots as represented by: where xi represents location of ith data point (knot), ai, bi, ci, and di are constants to be determined for the function si(x) between ith and (i+1)th knots. These constants in the polynomial can be solved by a system of equations derived by satisfying the following conditions: a) Continuity condition, i.e., the function must pass through all the points. b) The function values of adjacent polynomials must be equation at the knots. c) The first derivatives at the interior nodes must be equal. d) End conditions at the first and last nodes