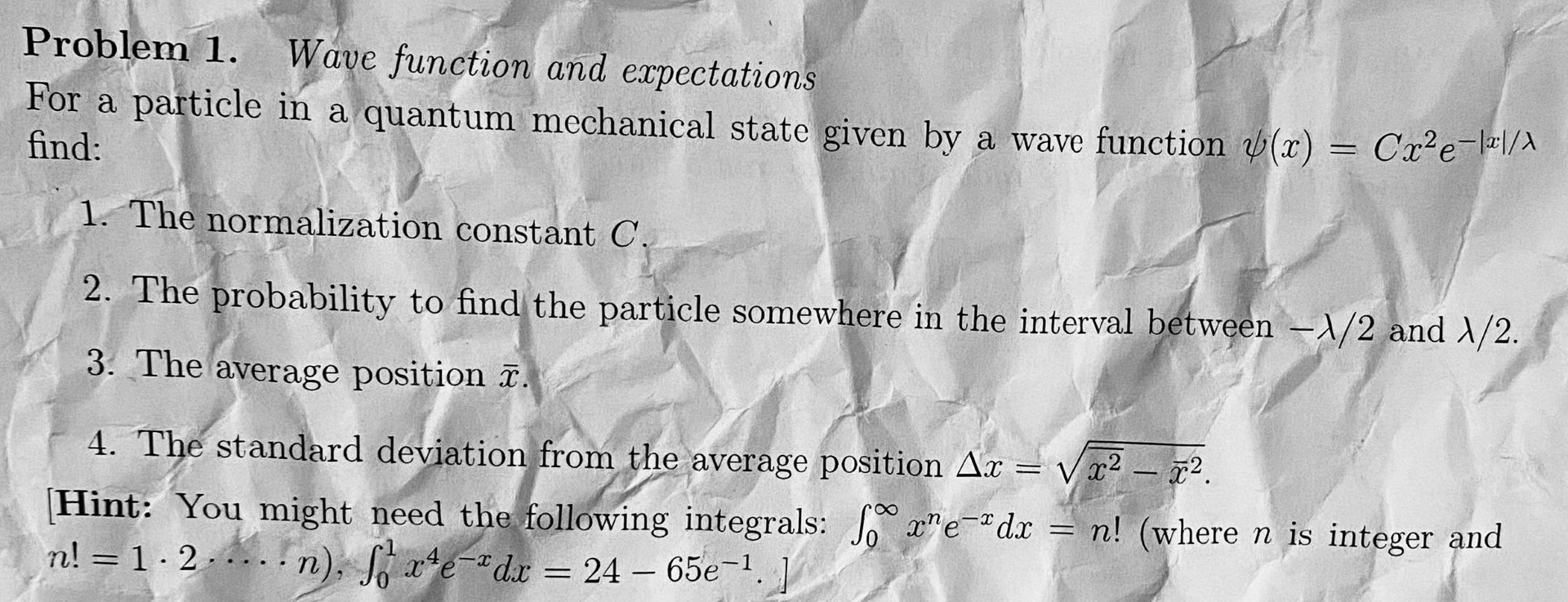
Problem 1. Wave function and expectations For a particle in a quantum mechanical state given by a wave function (x) = C'x2e-lz1/1 find: 1. The normalization constant C. 2. The probability to find the particle somewhere in the interval between -1/2 and 1/2. 3. The average position T. 4. The standard deviation from the average position Ax = V x2 - x2. Hint: You might need the following integrals: Jo xe Edx = n! (where n is integer and n! = 1 . 2 . ... .n), foxte "dx = 24 - 65e-1. ]