Problem 1)

Write a program that converts infix arithmetic expressions into a postfix form and then evaluates the resulting postfix expression (as described in the lecture notes). Use linked lists for the data structures.You must create your own Stack and Queue class.

Write the code and show example runs to prove that the program works as intended. Explain the data structures used.

LECTURE NOTES:

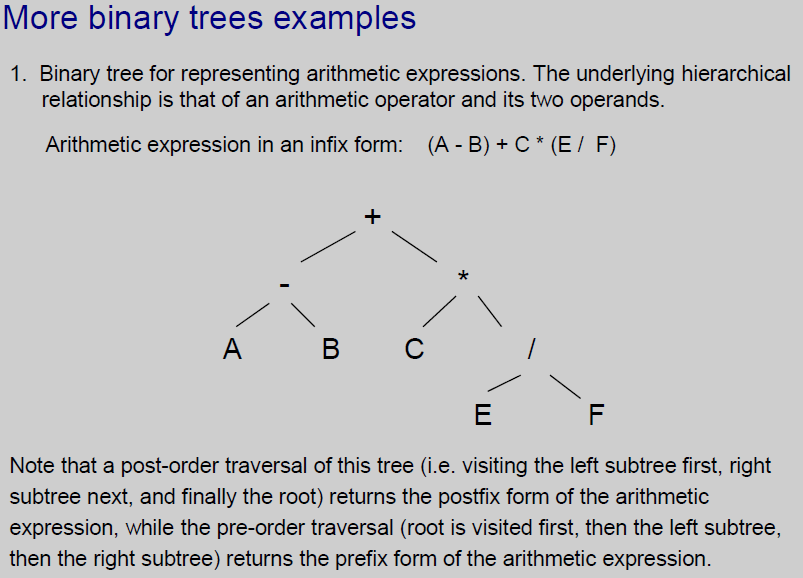
More binary trees examples 1. Binary tree for representing arithmetic expressions. The underlying hierarchical relationship is that of an arithmetic operator and its two operands Arithmetic expression in an infix form: (A - B) + C* (E/ F) BC Note that a post-order traversal of this tree (i.e. visiting the left subtree first, right subtree next, and finally the root) returns the postfix form of the arithmetic expression, while the pre-order traversal (root is visited first, then the left subtree, then the right subtree) returns the prefix form of the arithmetic expression More binary trees examples 1. Binary tree for representing arithmetic expressions. The underlying hierarchical relationship is that of an arithmetic operator and its two operands Arithmetic expression in an infix form: (A - B) + C* (E/ F) BC Note that a post-order traversal of this tree (i.e. visiting the left subtree first, right subtree next, and finally the root) returns the postfix form of the arithmetic expression, while the pre-order traversal (root is visited first, then the left subtree, then the right subtree) returns the prefix form of the arithmetic expression