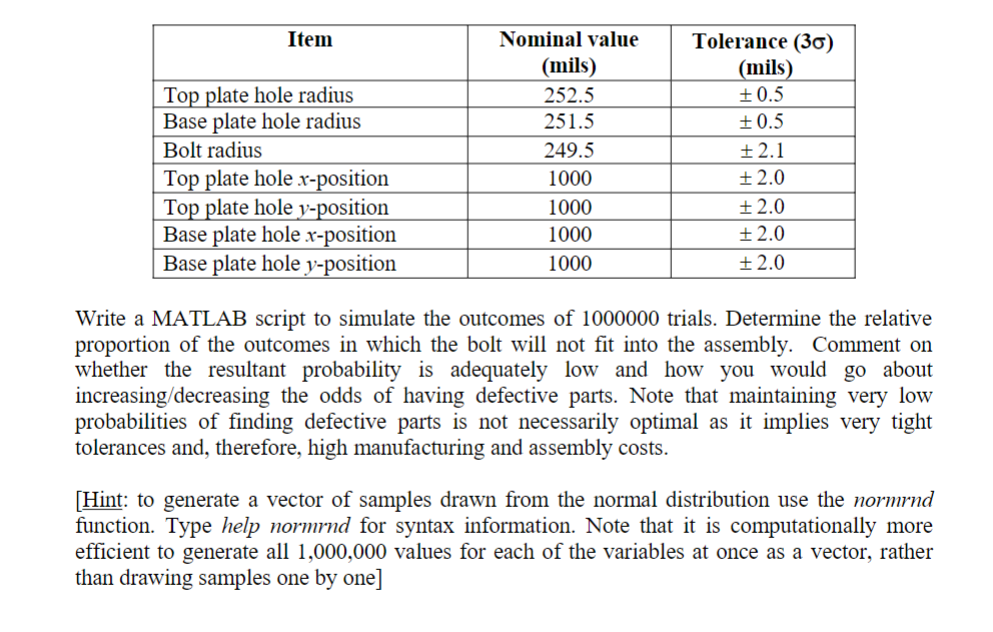
Problem 10 Monte Carlo analysis is a mathematical simulation of physical processes based on one's knowledge of the distributions of the process parameters. Monte Carlo simulations are used to predict the performance of complex physical systems that are subject to uncertainty and whose outcomes are controlled by the interaction of multiple independent factors. A three-component system, shown below, consists of a top plate, a base plate, and a bolt that must fit through holes in the two plates simultaneously. The top plate is not free to move relative to the base plate. Since there is variation in the diameters of the holes and bolt and in the true positions of the holes due to manufacturing and/or assembly tolerances, there will be some chance that the alignment will be off enough that the bolt will not fit through the two holes. Monte Carlo analysis can be used in this situation to determine the probability of an arbitrary set of components fitting together and evaluating the tolerance specifications on the individual components and the alignment process. a) If the radius of the hole in the top plate is rp, the radius of the hole in the base plate is rb, the bolt diameter is d, and the relative misalignment of the two holes is r, determine the geometric criterion that can be used to determine whether the bolt will or will not fit into the assembly. Consider the following two cases: rrprb and rrprb, as the "fitting" criterion is different for the two cases. Refer to the diagram for details. b) The table below contains the nominal dimensions and 3 tolerance limits for the radii of the two holes, the diameter of the bolt, and the x and y coordinates of the two holes measured with respect to some reference point. It is assumed that all the dimensions and coordinates are normally distributed. Write a MATLAB script to simulate the outcomes of 1000000 trials. Determine the relative proportion of the outcomes in which the bolt will not fit into the assembly. Comment on whether the resultant probability is adequately low and how you would go about increasing/decreasing the odds of having defective parts. Note that maintaining very low probabilities of finding defective parts is not necessarily optimal as it implies very tight tolerances and, therefore, high manufacturing and assembly costs. [Hint: to generate a vector of samples drawn from the normal distribution use the normrnd function. Type help normrnd for syntax information. Note that it is computationally more efficient to generate all 1,000,000 values for each of the variables at once as a vector, rather than drawing samples one by one]