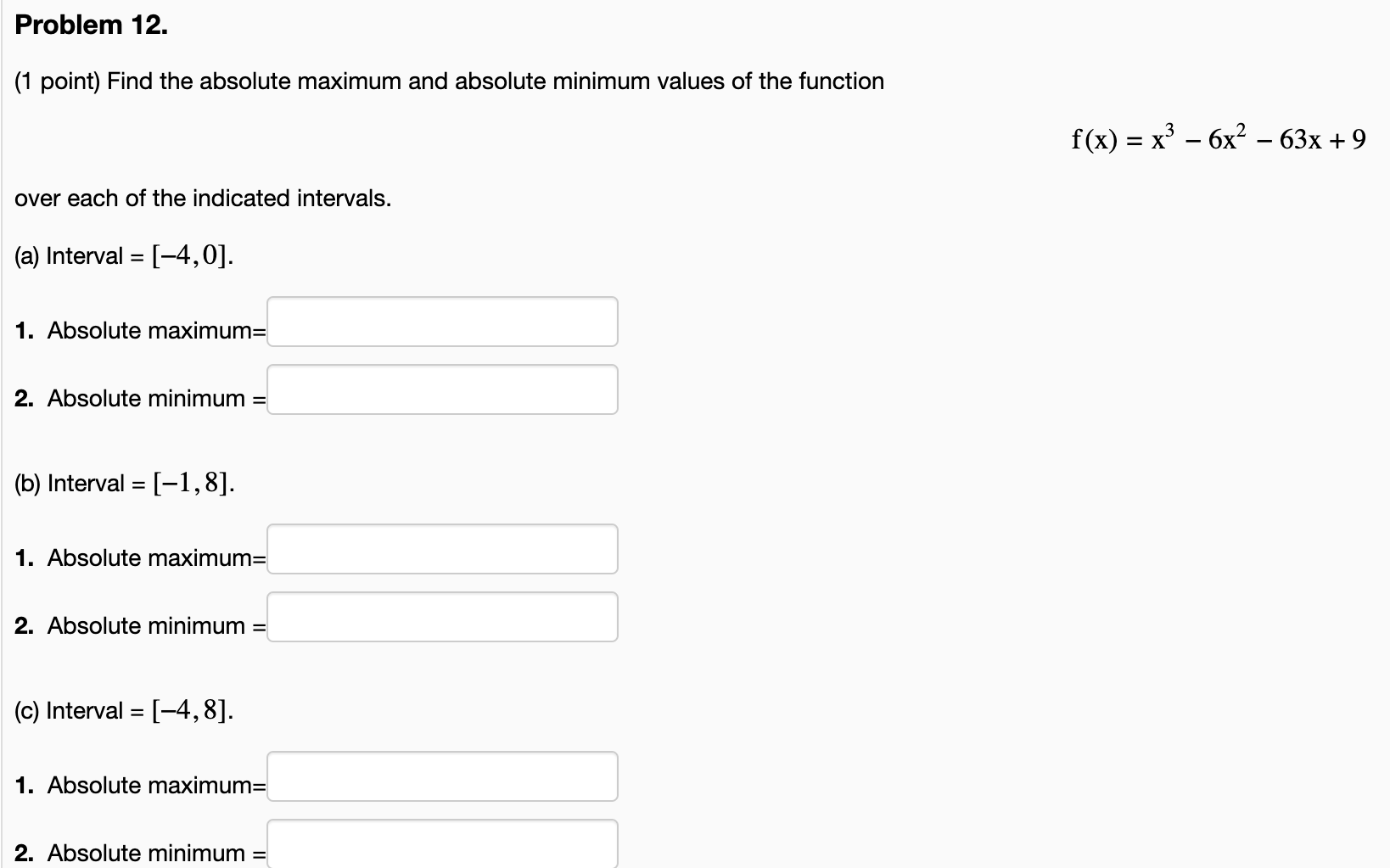
Question: Problem 12. (1 point) Find the absolute maximum and absolute minimum values of the function f(x) = x3 6x2 63x + 9 over each of
![each of the indicated intervals. (a) Interval = [4,0]. 1. Absolute maximum:](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6665aa5012c2a_7676665aa4fe9371.jpg)
![2. Absolute minimum : (b) Interval = [1, 8]. 1. Absolute maximum:](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6665aa5066418_7686665aa5048249.jpg)
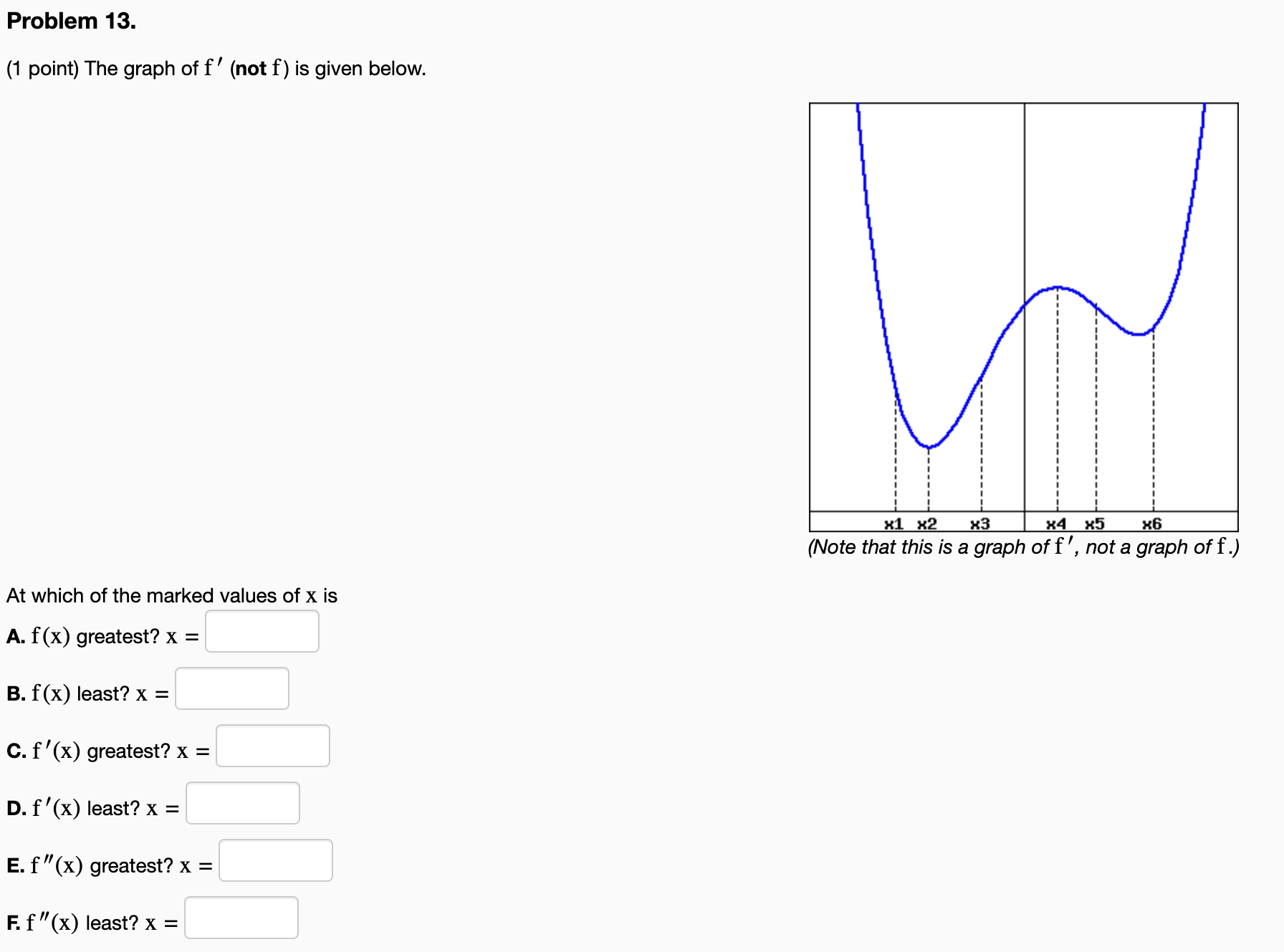
Problem 12. (1 point) Find the absolute maximum and absolute minimum values of the function f(x) = x3 6x2 63x + 9 over each of the indicated intervals. (a) Interval = [4,0]. 1. Absolute maximum: 2. Absolute minimum : (b) Interval = [1, 8]. 1. Absolute maximum: 2. Absolute minimum : (c) Interval = [4, 8]. 1. Absolute maximum: 2. Absolute minimum : Problem 13. (1 point) The graph of f ' (not f) is given below. xi x2 83 x4 x5 x6 (Note that this is a graph of f ', not a graph of f.) At which of the marked values of X is A. f (x) greatest? x = B. f (x) least? x = C. f '(X) greatest? X = D. f ' (X) least? x = E. f '"(x) greatest? x = F. f \"(x) least? x =
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


