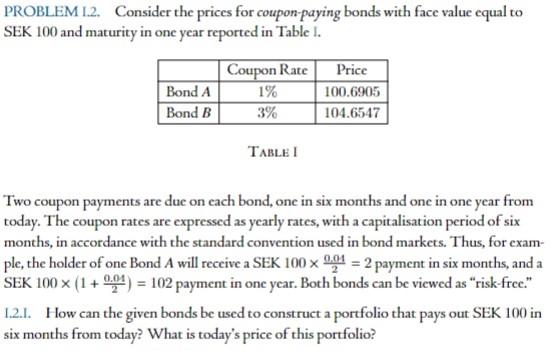
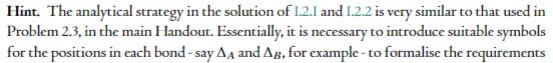
PROBLEM 1.2. Consider the prices for coupon-paying bonds with face value equal to SEK 100 and maturity in one year reported in Table I. Bond A Bond B Coupon Rate Price 1% 100.6905 3% 104.6547 TABLET Two coupon payments are due on cach bond, one in six months and one in one year from today. The coupon rates are expressed as yearly rates, with a capitalisation period of six months, in accordance with the standard convention used in bond markets. Thus, for exam- ple, the holder of one Bond A will receive a SEK 100 x 9,01 = 2 payment in six months, and a SEK 100 x (1 + 0,04) = 102 payment in one year. Both bonds can be viewed as "risk-frce." 1.2.1. How can the given bonds be used to construct a portfolio that pays out SEK 100 in six months from today? What is today's price of this portfolio? Hint. The analytical strategy in the solution of 1.2.1 and 1.2.2 is very similar to that used in Problem 2.3, in the main Handout. Essentially, it is necessary to introduce suitable symbols for the positions in each bond-say AA and AB, for example-to formalise the requirements that the cash-flows faced in six months and in one year from today are equal to the desired ones. The system thereby obtained should then be solved for AA and AB. Recall that the values of AA and Ag that solve the system Jax AA+b X A8 = oa, (exAA+ d x Ag = 0B. where a xd #bx c, are expressed by dx - bx = axd-bxc - AB axd-bxc In 1.2.5, the algebra can be simplified by setting R6 = e Post and R12 = 0,2**. This convention makes it possible to write the system formed by the two present value-equations as a linear system. e PROBLEM 1.2. Consider the prices for coupon-paying bonds with face value equal to SEK 100 and maturity in one year reported in Table I. Bond A Bond B Coupon Rate Price 1% 100.6905 3% 104.6547 TABLET Two coupon payments are due on cach bond, one in six months and one in one year from today. The coupon rates are expressed as yearly rates, with a capitalisation period of six months, in accordance with the standard convention used in bond markets. Thus, for exam- ple, the holder of one Bond A will receive a SEK 100 x 9,01 = 2 payment in six months, and a SEK 100 x (1 + 0,04) = 102 payment in one year. Both bonds can be viewed as "risk-frce." 1.2.1. How can the given bonds be used to construct a portfolio that pays out SEK 100 in six months from today? What is today's price of this portfolio? Hint. The analytical strategy in the solution of 1.2.1 and 1.2.2 is very similar to that used in Problem 2.3, in the main Handout. Essentially, it is necessary to introduce suitable symbols for the positions in each bond-say AA and AB, for example-to formalise the requirements that the cash-flows faced in six months and in one year from today are equal to the desired ones. The system thereby obtained should then be solved for AA and AB. Recall that the values of AA and Ag that solve the system Jax AA+b X A8 = oa, (exAA+ d x Ag = 0B. where a xd #bx c, are expressed by dx - bx = axd-bxc - AB axd-bxc In 1.2.5, the algebra can be simplified by setting R6 = e Post and R12 = 0,2**. This convention makes it possible to write the system formed by the two present value-equations as a linear system. e