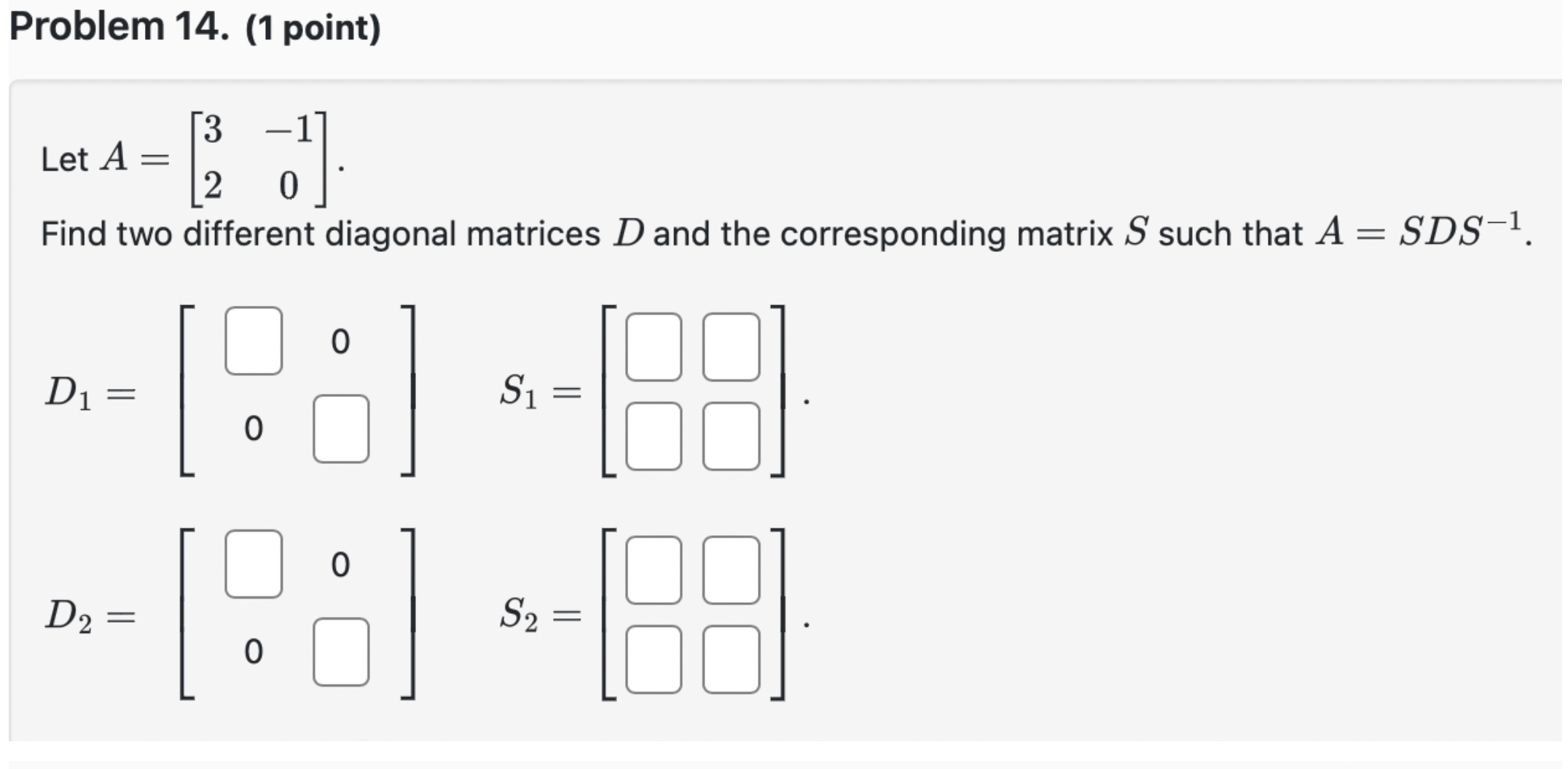
Problem 13. (1 point) Let A be a 3 x 3 diagonalizable matrix whose eigenvalues are 1 = 2, 12 = -3, and 13 = 4. If v1 = [1 0 0], v2 = [1 1 0], v3 = [0 1 1] are eigenvectors of A corresponding to /1, 12, and 13, respectively, then factor A into a product XDX- with D diagonal, and use this factorization to find A.Problem 14. (1 point) 3 1 A = . Let [2 0] Find two different diagonal matrices D and the corresponding matrix S such that A = SDS'I. [3 D1 C] if mm mm C] D D I? || C [j E,\" ||