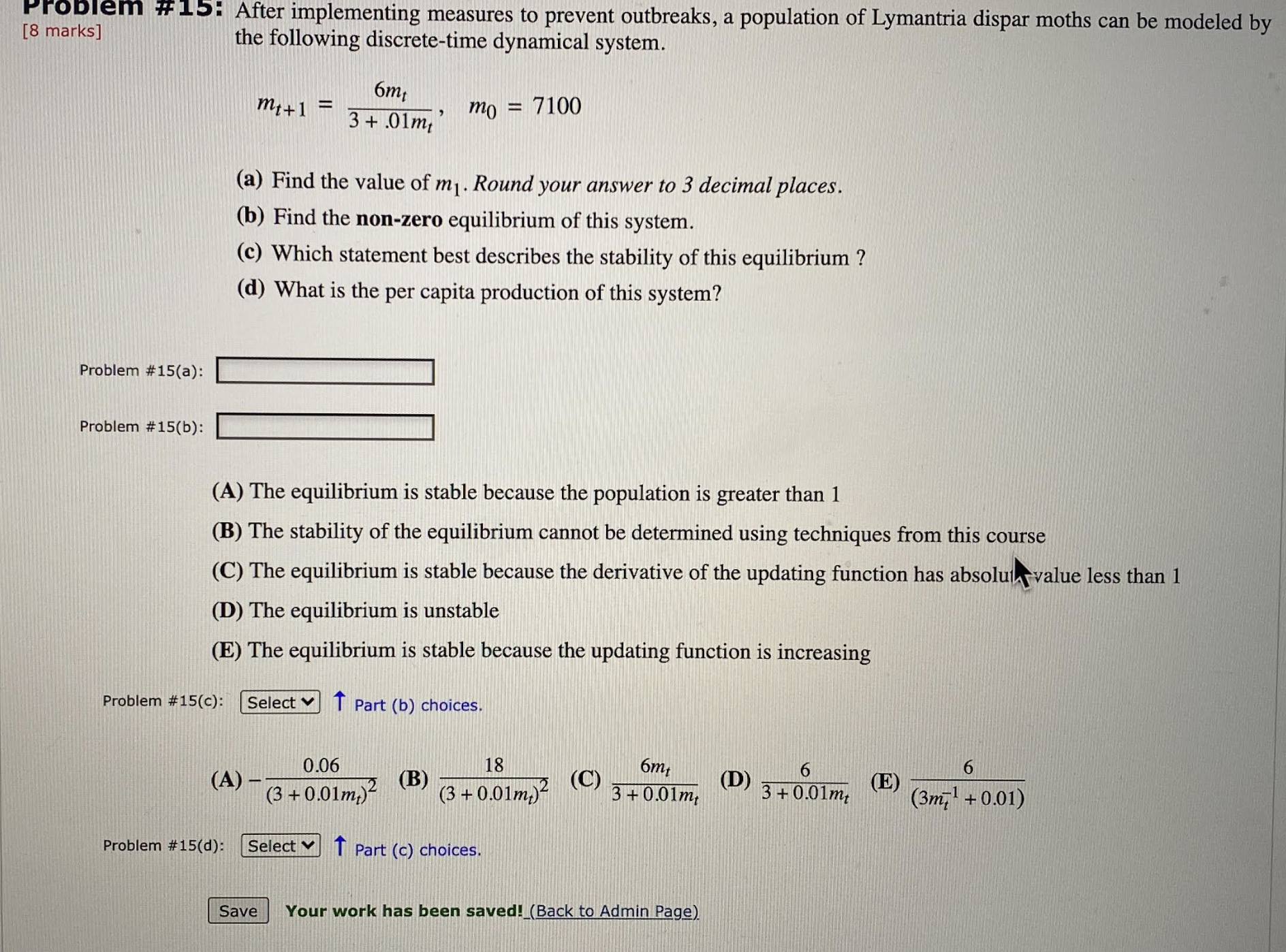
Question: Problem #15: After implementing measures to prevent outbreaks, a population of Lymantria dispar moths can be modeled by [8 marks] the following discrete-time dynamical system.
![Lymantria dispar moths can be modeled by [8 marks] the following discrete-time](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6679d25eabcd7_7426679d25e3c9d2.jpg)
Problem #15: After implementing measures to prevent outbreaks, a population of Lymantria dispar moths can be modeled by [8 marks] the following discrete-time dynamical system. 6mt mi+ 1 - mo = 7100 3 + .01mt (a) Find the value of m1. Round your answer to 3 decimal places. (b) Find the non-zero equilibrium of this system. (c) Which statement best describes the stability of this equilibrium ? (d) What is the per capita production of this system? Problem #15(a): Problem # 15(b): (A) The equilibrium is stable because the population is greater than 1 (B) The stability of the equilibrium cannot be determined using techniques from this course (C) The equilibrium is stable because the derivative of the updating function has absolut value less than 1 (D) The equilibrium is unstable (E) The equilibrium is stable because the updating function is increasing Problem # 15(c): Select v T Part (b) choices. 0.06 18 6mt 6 6 (A) - (B) (3 + 0.01my- (C) (D) 3 +0.01mt 3 + 0.01mt (E) (3 +0.01mt) (3m,] + 0.01) Problem # 15(d): Select v T Part (c) choices. Save Your work has been saved!_(Back to Admin Page)
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


