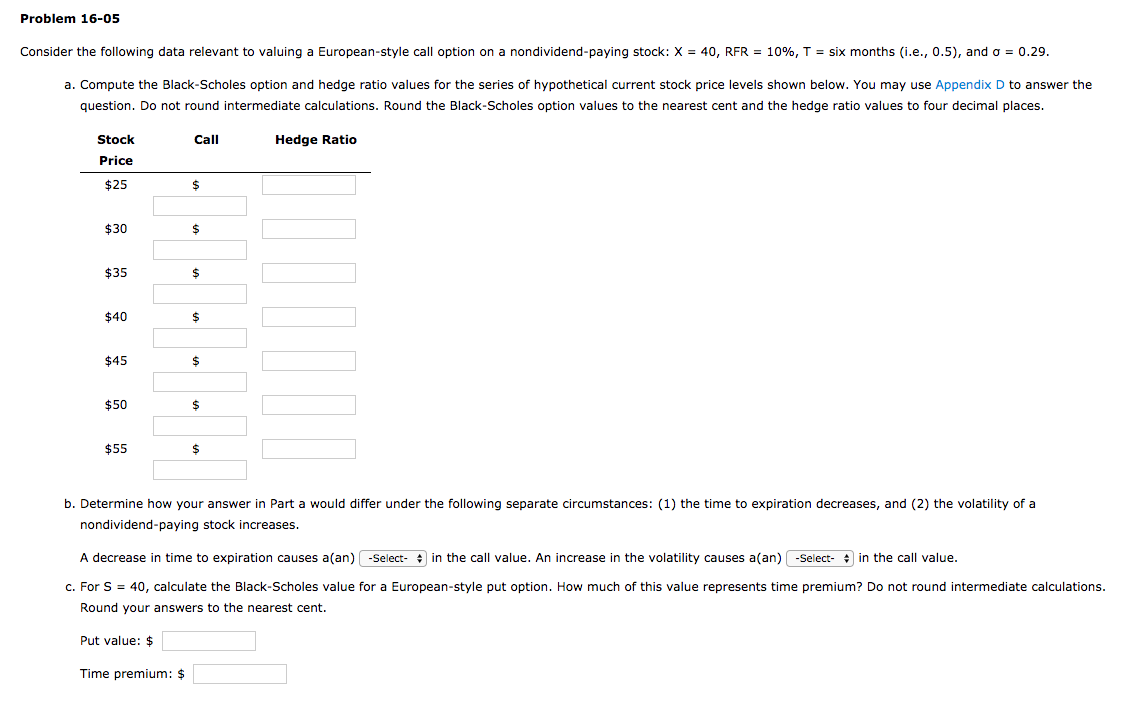
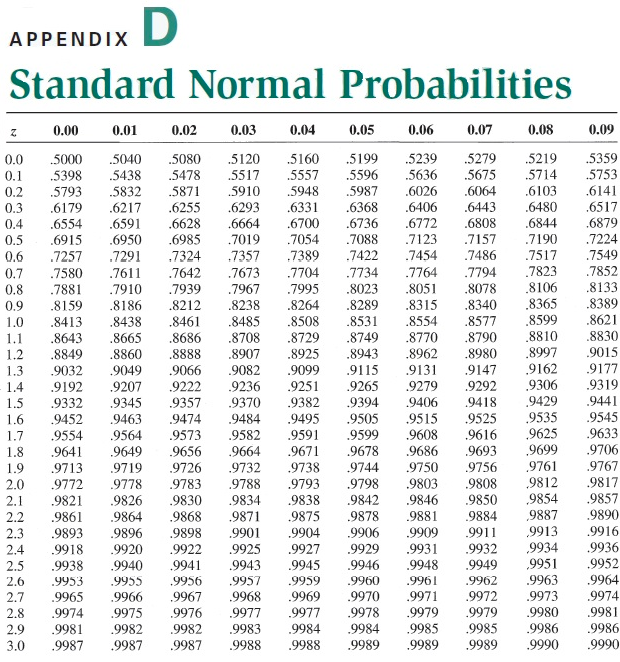
Problem 16-05 Consider the following data relevant to valuing a European-style call option on a nondividend-paying stock: X = 40, RFR = 10%, T = six months i.e., 0.5), and o = 0.29. a. Compute the Black-Scholes option and hedge ratio values for the series of hypothetical current stock price levels shown below. You may use Appendix D to answer the question. Do not round intermediate calculations. Round the Black-Scholes option values to the nearest cent and the hedge ratio values to four decimal places. Stock Call Hedge Ratio b. Determine how your answer in Part a would differ under the following separate circumstances: (1) the time to expiration decreases, and (2) the volatility of a nondividend-paying stock increases. A decrease in time to expiration causes a(an) -Select- in the call value. An increase in the volatility causes a(an) -Select- in the call value. c. For S = 40, calculate the Black-Scholes value for a European-style put option. How much of this value represents time premium? Do not round intermediate calculations. Round your answers to the nearest cent. Put value: $ Time premium: $ APPENDIX D Standard Normal Probabilities Z 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.0 0.1 0.2 .5987 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 - 1.4 5000 5040 .5080 5120 5160 .5199 .5239 .5279 .5219 .5359 .5398 .5438 .5478 5517 5557 .5596 .5636 .5675 .5714 .5753 .5793 5832 .5871 5910 5948 .6026 .6064 .6103 .6141 .6179 .6217 .6255 .6293 .6331 .6368 .6406 .6443 .6480 .6517 .6554 .6591 .6628 .6664 6700 .6736 .6772 .6808 .6844 .6879 .6915 .6950 .6985 .7019 .7054 .7088 .7123 .7157 .7190 .7224 .7257 .7291 .7324 .7357 .7389 .7422 .7454 .7486 .7517 .7549 .7580 .7611 .7642 .7673 .7704 .7734 .7764 .7794 .7823 .7852 .7881 .7910 .7939 .7967 .7995 .8023 .8051 .8078 .8106 .8133 .8159 .8186 .8212 .8238 .8264 .8289 .8315 .8340 .8365 .8389 .8413 .8438 .8461 .8485 .8508 .8531 .8554 .8577 .8599 .8621 .8643 .8665 .8686 .8708 .8729 .8749 .8770 .8790 .8810 .8830 .8849 .8860 .8888 .8907 .8925 .8943 .8962 .8980 .8997 .9015 .9032 .9049 .9066 9082 .9099 .9115 9131 .9147 9162 9177 .9192 9207 9222 9236 .9251 .9265 .9279 9292 9306 .9319 9332 9345 .9357 9370 .9382 .9394 9406 .9418 9429 .9452 9463 9474 9484 .9495 .9505 9515 .9525 .9535 9545 9554 9564 .9573 9582 9591 .9599 9608 .9616 9625 .9633 .9641 9649 9656 .9664 9671 9678 9686 .9693 .9699 .9706 97139719 .9726 9732 .9738 9744 .9750 9756 9761 .9767 .9772 .9778 9783 9788 .9793 .9798 9803 .9808 9812 .9817 .9821 .9826 .9830 9834 9838 .9842 9846 9850 9854 9857 .9861 .9864 .9868 9871 .9875 .9878 .9881 .9884 9887 .9890 .9893 .9896 9898 9901 9904 .9906 9909 .9911 9913 .9916 .9918 .9920 9922 9925 9927 .9929 .9931 9932 9934 .9936 .9938 .9940 .9941 .9943 .9945 .9946 9948 9949 ,9951 .9952 .9953 9955 .9956 .9957 9959 .9960 .9961 9962 .9963 9964 .9965 9966 9967 9968 9969 .9970 .99719972 .9973 9974 .9974 .9975 9976 .9977 9977 .9978 .99799979 9980 9981 .9981 .9982 9982 9983 9984 .9984 .9985 9985 .9986 .9986 99879987998799889988 99899989998999909990 9441 2.7 2.8 2.9 3.0 Problem 16-05 Consider the following data relevant to valuing a European-style call option on a nondividend-paying stock: X = 40, RFR = 10%, T = six months i.e., 0.5), and o = 0.29. a. Compute the Black-Scholes option and hedge ratio values for the series of hypothetical current stock price levels shown below. You may use Appendix D to answer the question. Do not round intermediate calculations. Round the Black-Scholes option values to the nearest cent and the hedge ratio values to four decimal places. Stock Call Hedge Ratio b. Determine how your answer in Part a would differ under the following separate circumstances: (1) the time to expiration decreases, and (2) the volatility of a nondividend-paying stock increases. A decrease in time to expiration causes a(an) -Select- in the call value. An increase in the volatility causes a(an) -Select- in the call value. c. For S = 40, calculate the Black-Scholes value for a European-style put option. How much of this value represents time premium? Do not round intermediate calculations. Round your answers to the nearest cent. Put value: $ Time premium: $ APPENDIX D Standard Normal Probabilities Z 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.0 0.1 0.2 .5987 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 - 1.4 5000 5040 .5080 5120 5160 .5199 .5239 .5279 .5219 .5359 .5398 .5438 .5478 5517 5557 .5596 .5636 .5675 .5714 .5753 .5793 5832 .5871 5910 5948 .6026 .6064 .6103 .6141 .6179 .6217 .6255 .6293 .6331 .6368 .6406 .6443 .6480 .6517 .6554 .6591 .6628 .6664 6700 .6736 .6772 .6808 .6844 .6879 .6915 .6950 .6985 .7019 .7054 .7088 .7123 .7157 .7190 .7224 .7257 .7291 .7324 .7357 .7389 .7422 .7454 .7486 .7517 .7549 .7580 .7611 .7642 .7673 .7704 .7734 .7764 .7794 .7823 .7852 .7881 .7910 .7939 .7967 .7995 .8023 .8051 .8078 .8106 .8133 .8159 .8186 .8212 .8238 .8264 .8289 .8315 .8340 .8365 .8389 .8413 .8438 .8461 .8485 .8508 .8531 .8554 .8577 .8599 .8621 .8643 .8665 .8686 .8708 .8729 .8749 .8770 .8790 .8810 .8830 .8849 .8860 .8888 .8907 .8925 .8943 .8962 .8980 .8997 .9015 .9032 .9049 .9066 9082 .9099 .9115 9131 .9147 9162 9177 .9192 9207 9222 9236 .9251 .9265 .9279 9292 9306 .9319 9332 9345 .9357 9370 .9382 .9394 9406 .9418 9429 .9452 9463 9474 9484 .9495 .9505 9515 .9525 .9535 9545 9554 9564 .9573 9582 9591 .9599 9608 .9616 9625 .9633 .9641 9649 9656 .9664 9671 9678 9686 .9693 .9699 .9706 97139719 .9726 9732 .9738 9744 .9750 9756 9761 .9767 .9772 .9778 9783 9788 .9793 .9798 9803 .9808 9812 .9817 .9821 .9826 .9830 9834 9838 .9842 9846 9850 9854 9857 .9861 .9864 .9868 9871 .9875 .9878 .9881 .9884 9887 .9890 .9893 .9896 9898 9901 9904 .9906 9909 .9911 9913 .9916 .9918 .9920 9922 9925 9927 .9929 .9931 9932 9934 .9936 .9938 .9940 .9941 .9943 .9945 .9946 9948 9949 ,9951 .9952 .9953 9955 .9956 .9957 9959 .9960 .9961 9962 .9963 9964 .9965 9966 9967 9968 9969 .9970 .99719972 .9973 9974 .9974 .9975 9976 .9977 9977 .9978 .99799979 9980 9981 .9981 .9982 9982 9983 9984 .9984 .9985 9985 .9986 .9986 99879987998799889988 99899989998999909990 9441 2.7 2.8 2.9 3.0