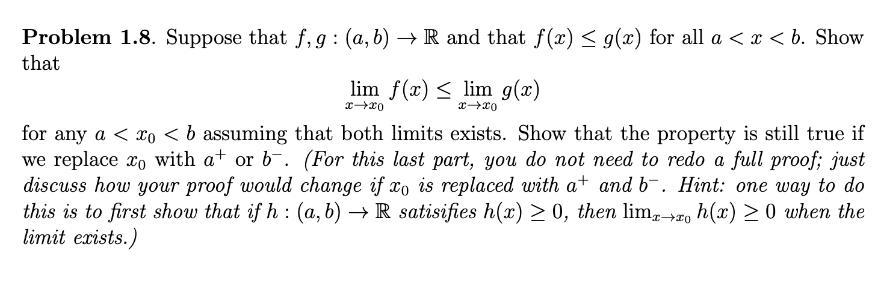
Problem 1.8. Suppose that f, g: (a, b) R and that f(x) g(x) for all a < x < b. Show that lim f(x) x-x0 lim g(x) x-xo for any a < xo < b assuming that both limits exists. Show that the property is still true if we replace to with at or b. (For this last part, you do not need to redo a full proof; just discuss how your proof would change if xo is replaced with at and b. Hint: one way to do this is to first show that if h: (a, b) R satisifies h(x) > 0, then limxzo h(x) 0 when the limit exists.)