Problem $2(18$ points$)$

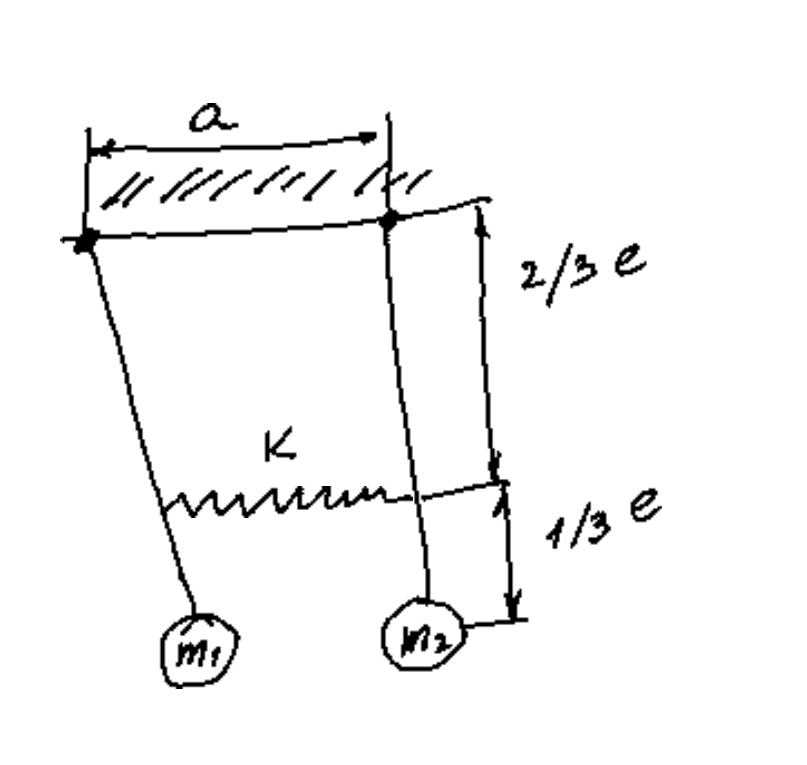
The two pendulums of the masses, $\backslash ($ m$\_\{1\}\backslash )$ and $\backslash ($ m$\_\{2\}\backslash ),$ are initially separated by a distance, $\backslash ($ a $\backslash ),$ and are connected to the base by rods of the length $\backslash ($ l $\backslash ).$ The rods are link to each other with a spring of the stiffness, $\backslash ($ k $\backslash ).$ The distance from the mass to the spring is $\backslash (1/3$ l $\backslash ).$ The spring is unstrained when the two pendulum rods are in the vertical position. Consider the free vibrations of the system.

$1)$ Use Newton's laws to derive equations of motion of the two$-$pendulum system WITHOUT the assumption of small angular displacement $\backslash (\backslash$theta $\backslash ).$ Specify initial conditions and values for the parameters of the system $\backslash ((\backslash$mathrm$\{$m$\},\backslash$mathrm$\{$k$\},\backslash$mathrm$\{$c$\})\backslash ).$ Write Matlab program computing non$-$linear time response of pendulums by using ODE$45.(6$ points$)$

$2)$ Derive equations of motion of the two$-$pendulum system WITH the assumption of small angular displacements, $\backslash (\backslash$theta $\backslash ).$ Write the second part of the Matlab program computing linear time response. Submit your MATLAB program. Plot non$-$linear and linear responses on the same figure. Compare results and provide a short discussion. $(5$ points$)$

$3)$ Find natural frequencies of the system. $(2$ points$)$

$4)$ Determine mode shapes of the vibration. Provide a sketch illustrating these shapes. $(5$ points$)$