Problem 2 (60 points). There is an insulating material with a semi-spherical shape (half hollow sphere) of inner radius R1 and outer radius R2. This insulating material is used for tops of a high-temperature reactor. The temperature of the inner face of the sphere is of T1 and the temperature of the external face is T2, both in stationary state during the process. Find the model that describes the variation of temperature with respect to to the (radial) thickness of the spherical material at steady state. Terms: T1, internal face temperature, 132 C T2, external face temperature, 1430 C R1, internal radius, 1.35 m R2, external radius, 1.75 m q, Heat flux, 175 kW/m2 k, thermal conductivity, 0.015 kW/m*K Find: to. The process diagram. (2 points) b. Definition of variables. (2 points) c. constitutive relationships. (3 points) d. Model conditions. (3 points)

e

. The mathematical model that describes the temperature variation is as follows: (check that it is the one shown in equation 2) (25 points)

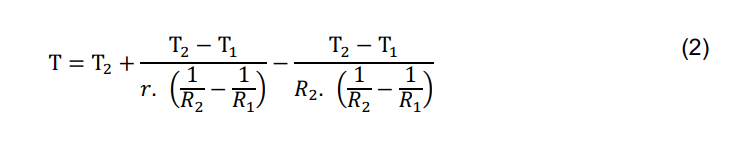F. Check the boundary conditions. (3 points) g. Dimensionally check your model. (2 points) h. From the model obtained in point "e", graph the value of the temperature from R2 to R1, with a step of 0.01 m between data. Perform a linear fit and a polynomial (degree 2, 3, 4, or other), and choose the one that best fits the data. Justify your choice. (single) (10 points) i. Propose an insulating material capable of withstanding the range of temperatures indicated in the problem, with its manufacturer's data sheet. (single) (10 points)

T2-T 1 1 (2) T = TS + T. - T 1 R2 R T ( 8 (3) )