Question: Problem 2 8 For the 3 DOF system shown with stiffnesses k 1 = k 2 = k 3 = 8 9 . 6 M
Problem
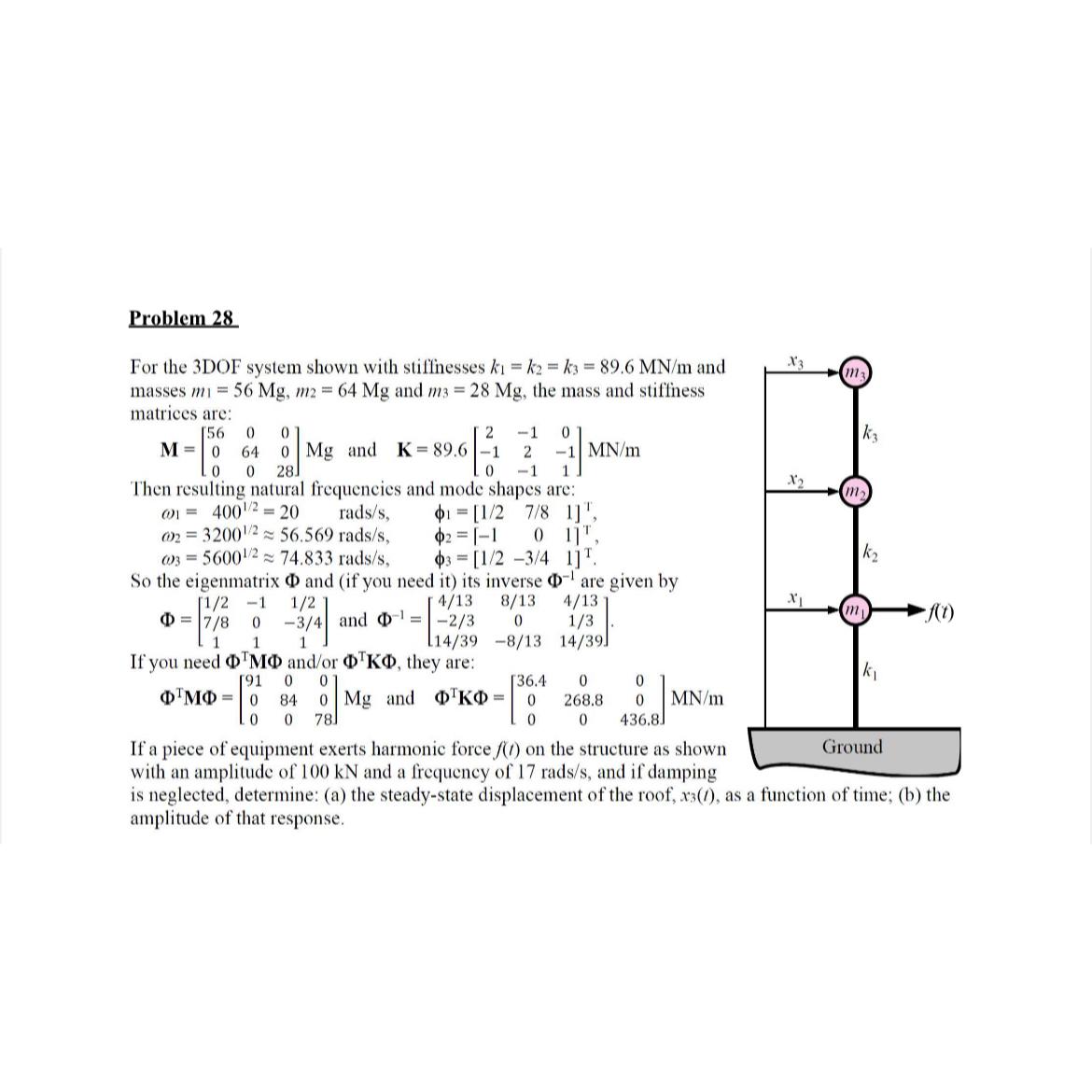
For the DOF system shown with stiffnesses and masses and the mass and stiffness matrices are:
and
Then resulting natural frequencies and mode shapes are:
rad
~~rad
~~rad
So the eigenmatrix and if you need it its inverse are given by
and
If you need andor they are:
and
If a piece of equipment exerts harmonic force on the structure as shown with an amplitude of and a frequency of rad and if damping is neglected, determine: a the steadystate displacement of the roof, as a function of time; b the amplitude of that response.
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


