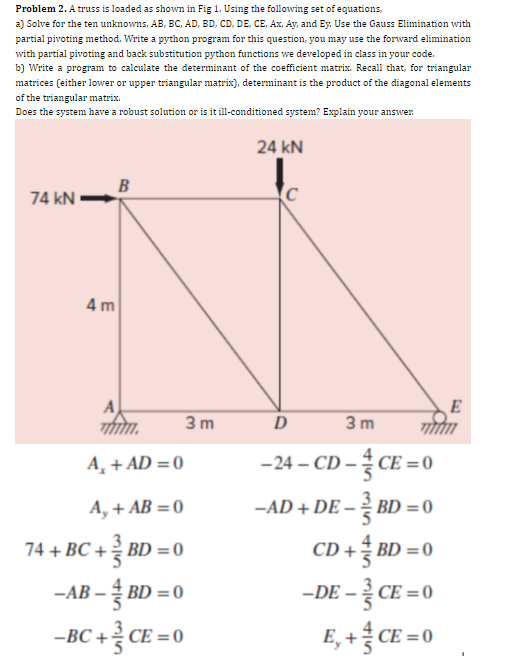
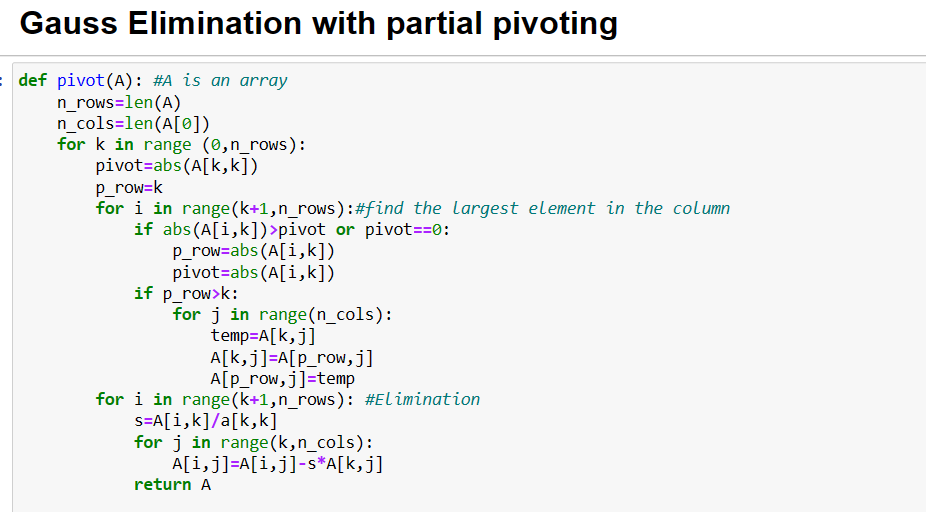
Problem 2. A truss is loaded as shown in Fig 1. Using the following set of equations, a) Solve for the ten unknowns, AB,BC,AD,BD,CD,DE,CE,Ax,Ay, and Ey, Use the Gauss Elimination with partial pivoting method. Write a python program for this question, you may use the forward elimination with partial pivoting and back substitution python functions we developed in class in your code. b) Write a program to calculate the determinant of the coefficient matrix. Recall that, for triangular matrices (either lower or upper triangular matrix), determinant is the product of the diagonal elements of the triangular matrix. Does the system have a robust solution or is it ill-conditioned system? Explain your answen Ax+AD=024CD54CE=0Ay+AB=0AD+DE53BD=074+BC+53BD=0CD+54BD=0AB54BD=0DE53CE=0BC+53CE=0Ey+54CE=0 Back Substitution import numpy as np def back substitution(AR): \#AR is augmented matrix append R into A) n= len (AR) \#number of unknowns =\# of rows of the augmented matrix AR X=np.zeros([n,1]) \#creates a column vecotr with n rows, filled with zeros X[n1]=AR[n1,n]/AR[n1,n1] for i in range (n1,1,1): sum=0 for j in range (i+1,n): x[i]=(AR[i,n]sum)/AR[i,j] Gauss Elimination with partial pivoting