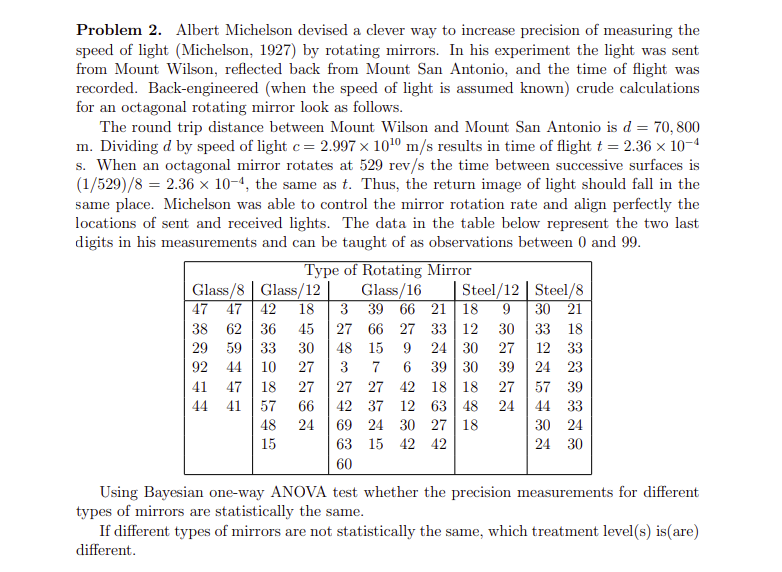
Problem 2. Albert Michelson devised a clever way to increase precision of measuring the speed of light (Michelson, 1927) by rotating mirrors. In his experiment the light was sent from Mount Wilson, reflected back from Mount San Antonio, and the time of flight was recorded. Back-engineered (when the speed of light is assumed known) crude calculations for an octagonal rotating mirror look as follows. The round trip distance between Mount Wilson and Mount San Antonio is d = 70, 800 m. Dividing d by speed of light c= 2.997 x 1010 m/s results in time of flight t = 2.36 x 10- s. When an octagonal mirror rotates at 529 rev/s the time between successive surfaces is (1/529)/8 = 2.36 x 10-4, the same as t. Thus, the return image of light should fall in the same place. Michelson was able to control the mirror rotation rate and align perfectly the locations of sent and received lights. The data in the table below represent the two last digits in his measurements and can be taught of as observations between () and 99. Type of Rotating Mirror Glass/8 | Glass/12 Glass/16 Steel/12 Steel/8 47 47 42 18 3 39 66 21 18 9 30 21 38 62 36 45 27 66 27 33 12 30 33 18 29 59 33 30 48 15 9 24 30 27 12 33 92 44 10 27 3 7 6 39 30 39 24 23 41 47 18 27 27 27 42 18 18 27 57 39 44 41 57 66 42 37 12 63 48 24 44 33 48 24 69 24 30 27 18 30 24 15 63 15 42 42 24 30 60 Using Bayesian one-way ANOVA test whether the precision measurements for different types of mirrors are statistically the same. If different types of mirrors are not statistically the same, which treatment level(s) is(are) different