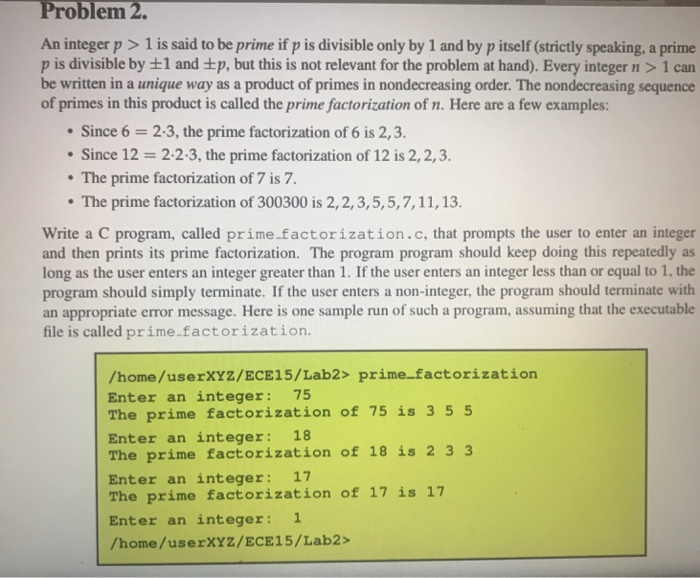
Problem 2 An integer p>1 is said to be prime if p is divisible only by 1 and by p itself (strictly speaking, a prime p is divisible by 1 and p, but this is not relevant for the problem at hand). Every integer n > 1 can be written in a unique way as a product of primes in nondecreasing order. The nondecreasing sequence of primes in this product is called the prime factorization of n. Here are a few examples: Since 6 2.3, the prime factorization of 6 is 2,3. . Since 12 = 2.23, the prime factorization of 12 is 2, 2, 3. The prime factorization of 7 is 7 The prime factorization of 300300 is 2,2,3,5,5,7,11,13. Write a C program, called prime.factorization.c, that prompts the user to enter an integer and then prints its prime factorization. The program program should keep doing this repeatedly as long as the user enters an integer greater than 1. If the user enters an integer less than or equal to 1, the program should simply terminate. If the user enters a non-integer, the program should terminate with an appropriate error message. Here is one sample run of such a program, assuming that the executable file is called prime.factorization. /home/userXY2/ECE15/Lab2> prime factorization Enter an integer 75 The prime factorization of 75 is 3 5 5 Enter an integer 18 The prime factorization of 18 is 2 3 3 Enter an integer 17 The prime factorization of 17 is 17 Enter an integer 1 /home/userXYZ/ECE15/Lab2>