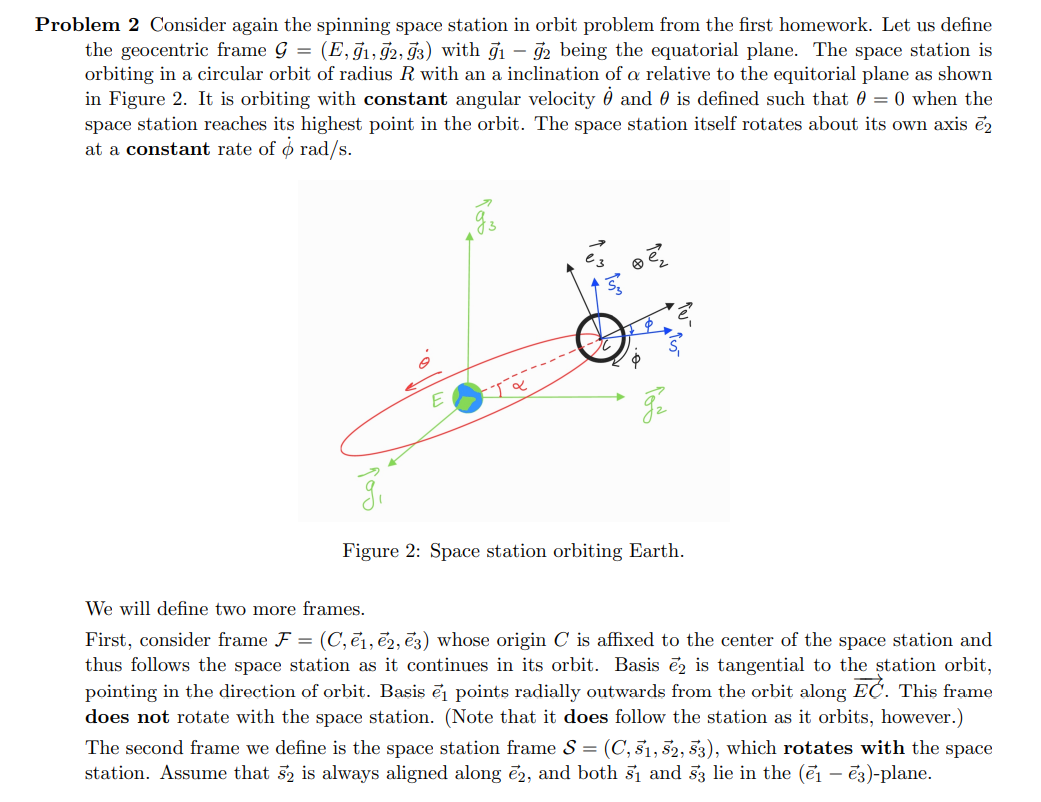
Problem 2 Consider again the spinning space station in orbit problem from the first homework. Let us define the geocentric frame G = (E,91,92, 93) with 9 - 92 being the equatorial plane. The space station is orbiting in a circular orbit of radius R with an a inclination of a relative to the equitorial plane as shown in Figure 2. It is orbiting with constant angular velocity and is defined such that 0 = 0 when the space station reaches its highest point in the orbit. The space station itself rotates about its own axis 2 at a constant rate of o rad/s. 9 Figure 2: Space station orbiting Earth. We will define two more frames. First, consider frame F = (C, , 2, 3) whose origin C is affixed to the center of the space station and thus follows the space station as it continues in its orbit. Basis 2 is tangential to the station orbit, pointing in the direction of orbit. Basis ei points radially outwards from the orbit along EC. This frame does not rotate with the space station. (Note that it does follow the station as it orbits, however.) The second frame we define is the space station frame S = (C, 51, 52, 53), which rotates with the space station. Assume that 32 is always aligned along 2, and both 5 and 53 lie in the (e - 3)-plane. (a) Is 2 = 9? If not, obtain an expression for 2 in terms of basis vectors of G. (Hint: See solutions for HW1) (b) We want to find the acceleration experienced by a person in the rotating ring of the space station. Consider a point P (not shown in figure) such that CP = rs where r is the radius of the space station. (P). (i) Find ve (C) and (ii) Find s/ and F/G (You may refer to what you did in HW1 here.) (iii) Use composition of acceleration to find ag(P). (c) We are now interested in calculating the 'artificial gravity' that a person at point P experiences. In the expression you obtained for ag(P), you will have one or more terms with ro in them. These term(s) correspond to the centripetal acceleration experienced by a person at P that's caused by the rotating space station. It will be balanced by a reaction force from the space station, creating the sensation of 'artificial gravity.' Let us call the term(s) with ro in them de. Then, the magnitude of 'artificial gravity' experienced by the person at P is simply |c.51. Compute the rotation rate o for the space station such that this magnitude |ac.51 | = 0.7 G. Assume r = 100 m and g = 9.8 m/s.