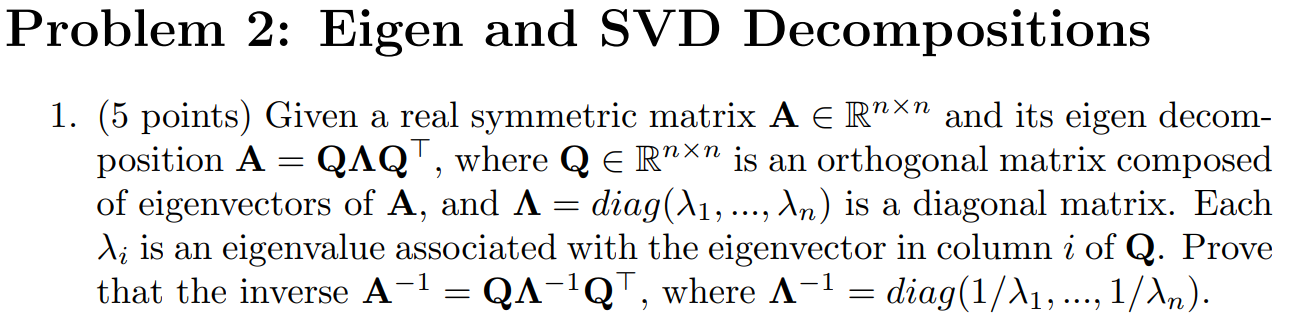
Problem 2: Eigen and SVD Decompositions 1. (5 points) Given a real symmetric matrix ARnn and its eigen decomposition A=QQ, where QRnn is an orthogonal matrix composed of eigenvectors of A, and =diag(1,,n) is a diagonal matrix. Each i is an eigenvalue associated with the eigenvector in column i of Q. Prove that the inverse A1=Q1Q, where 1=diag(1/1,,1)