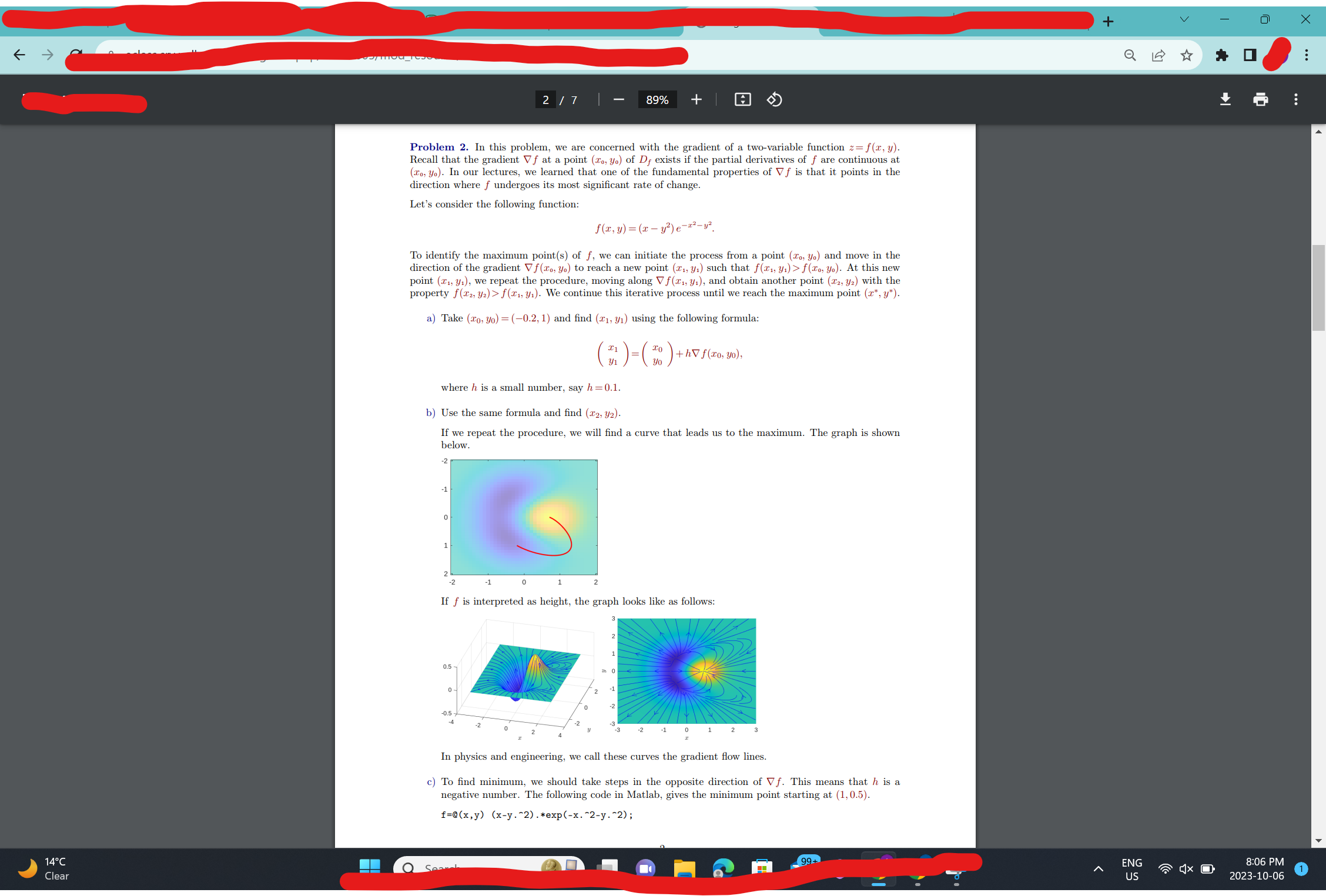
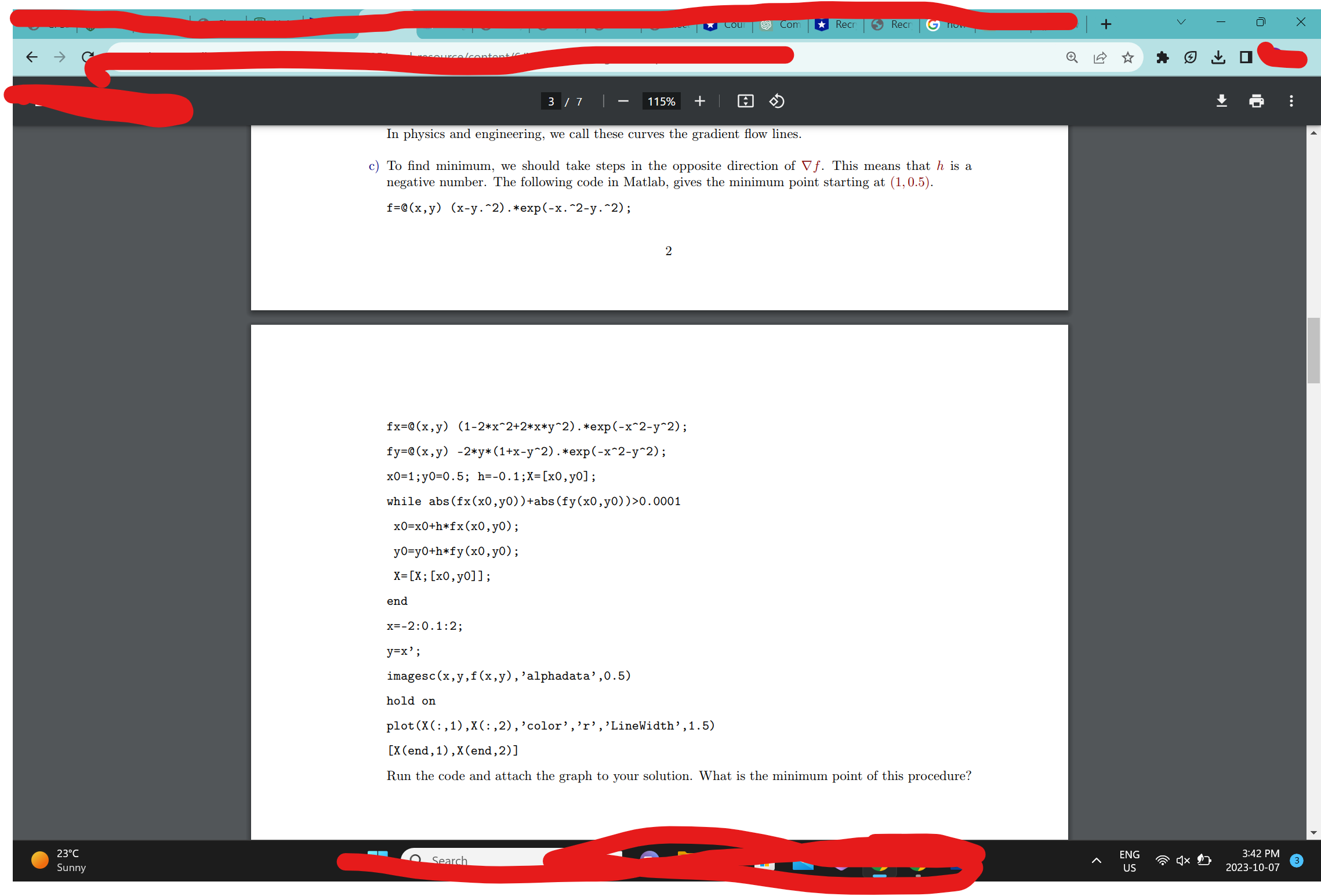
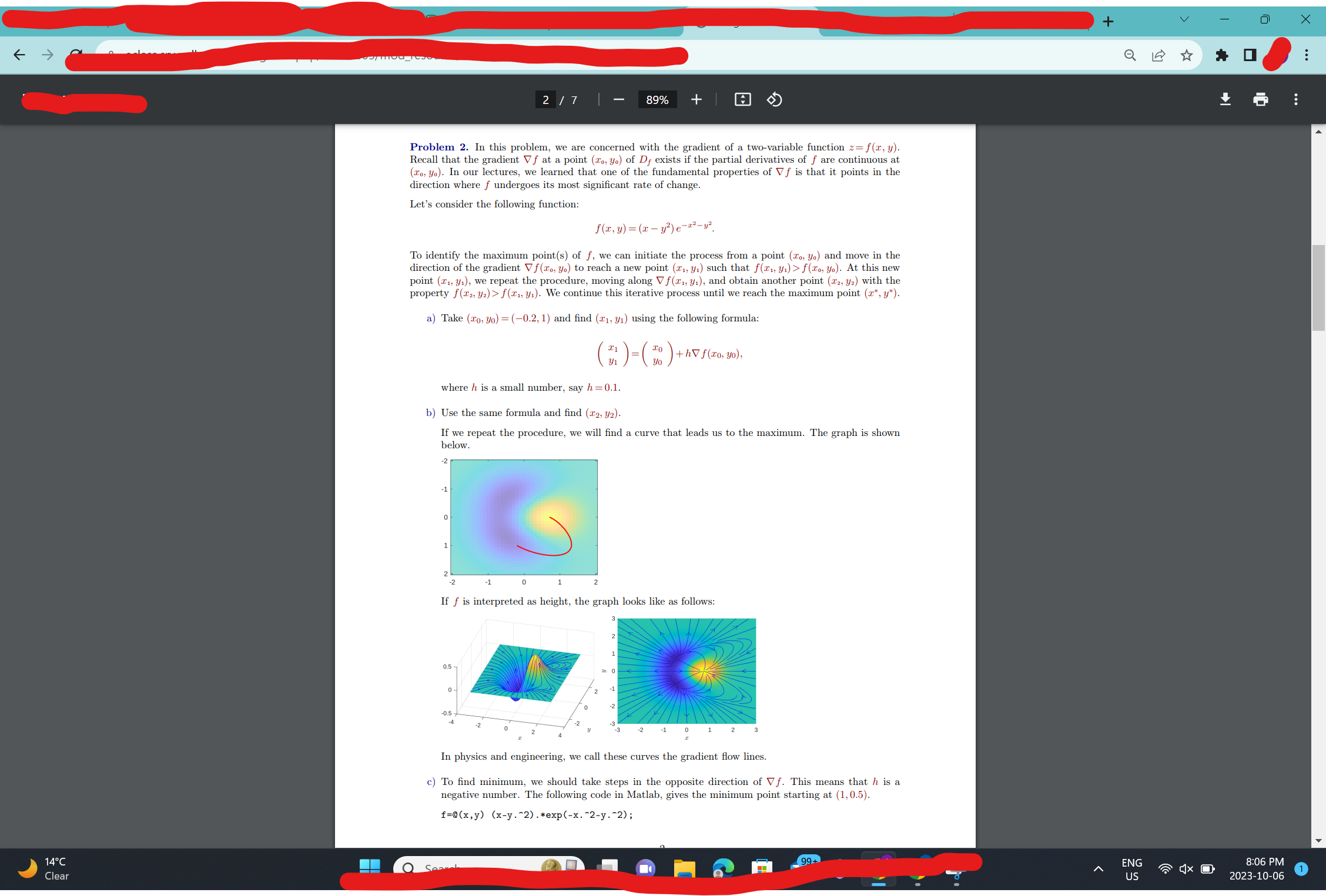
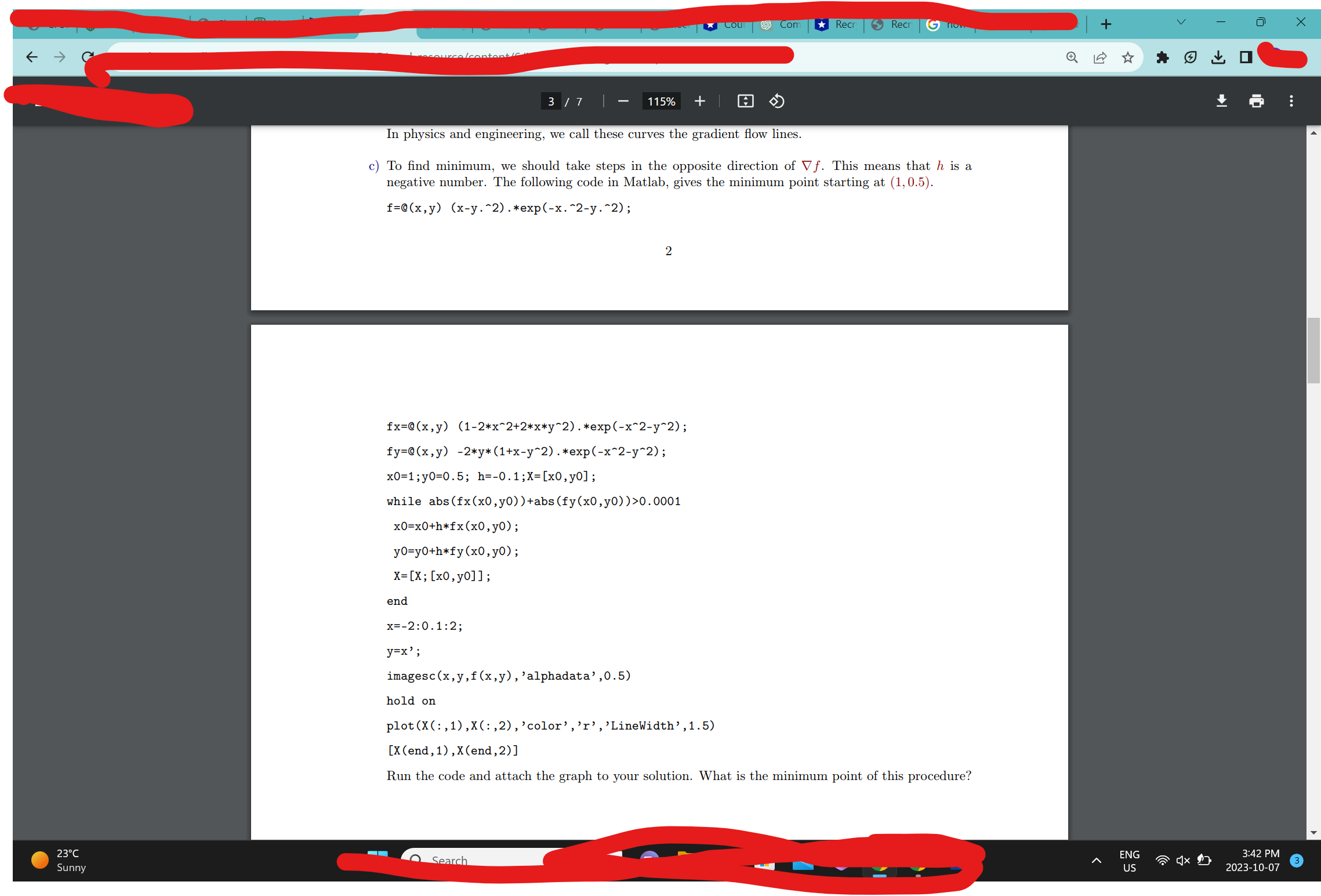
Problem 2' In this problem. we are concerned with the gradient of a two-Variable function 2: f(I. y). Recall that the gradient Y'f at a point (In. ya) of D, exists it the partial derivatives of f are continuous at (1,... y\") In our lectures. we learned that one of the fundamental properties of V f is that it points in the direction where / undergoes its most signicant rate of change. Let's consider the following function: f(r~y):(zr /2)e To identify the maximum point(s) of f. we can initiate the process from a point (n. ya) and move in the direction of the gradient Vfza. ya) to reach a new point (1,. yr) such that x, yi)>f(re. yo). At this new point (r,. y,). We repeat the procedure. moving along Vri. yr). and obtain another point (me. M) with the property [(cl. yr) > m, y.) We continue this iterative process until we reach the maximum point (If. y). a) Take (on. M.) : (en 2. 1) and nd (a) . y.) using the following furlnllla: (:3) where ll is a small number. say h :0.1. To ( W )+/1Vf(ru. ya). b) Use the same formula and nd (1, ll we repeat the procedure. we will nd a curve that leads us to the maximum. The graph is shown below -2 2 72 cl 0 i 2 ll f is interpreted as height. the graph looks like as follows: In physics and engineering. we call these curves the gradient ow lines. c) To nd minirnum. we should take steps in the opposite direction of Vf This means that n is a negative number. The following code in Matlab. gives the minimum point starting at (1.0 5). r=m0. 0001 x0=x0+h*fx(x0, yo) ; y0=y0th*fy (x0, yo) ; X=[X; [x0, y0] ] ; end x=-2:0. 1:2; y=x' ; imagesc (x, y, f (x,y), 'alphadata' , 0.5) hold on plot (X(: , 1) ,X(: ,2), 'color' , 'r' , 'LineWidth' , 1.5) [X (end, 1) , X (end, 2) ] Run the code and attach the graph to your solution. What is the minimum point of this procedure? 23.C ENG 3:42 PM Sunny Search US 2023-10-07 3