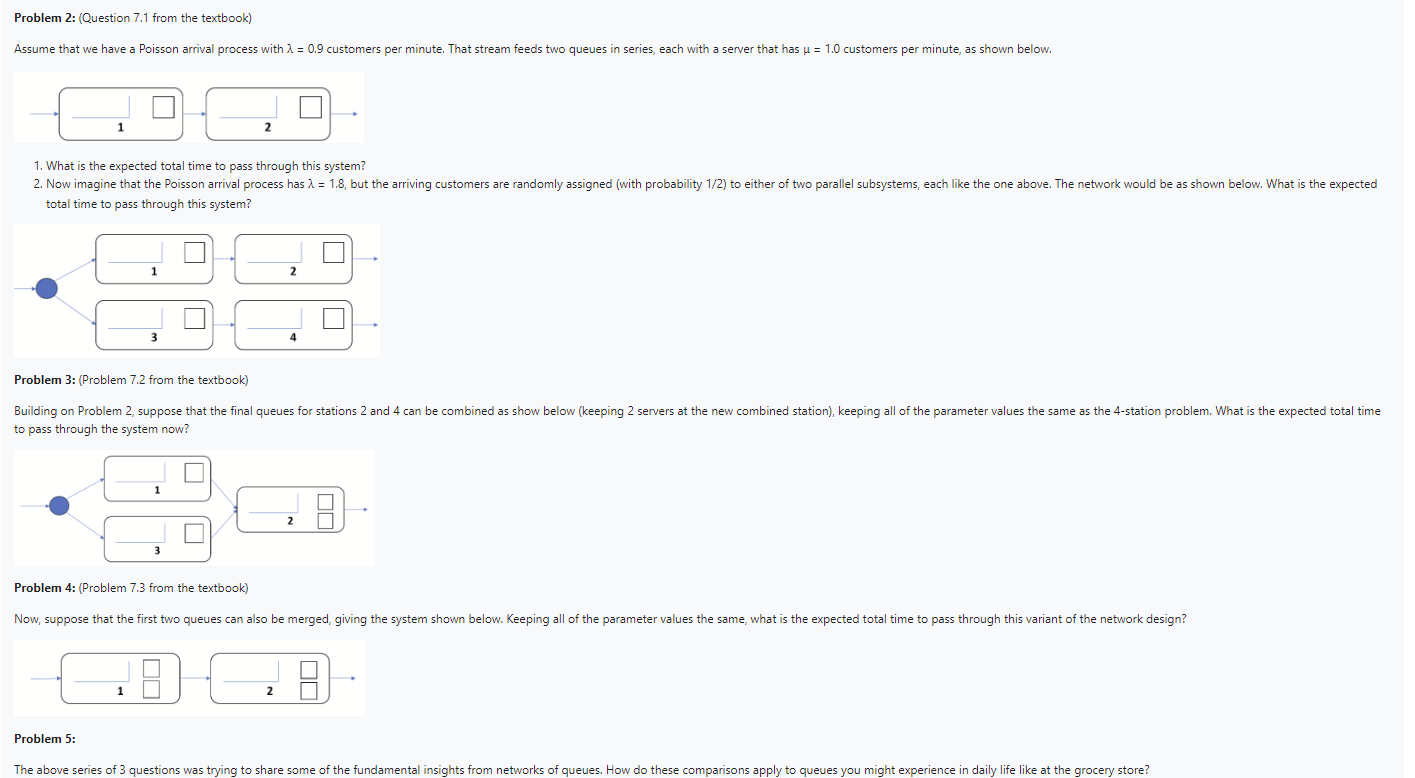
Problem $2$: $($Question $7\mathrm{.}1$ from the textbook$)$

Assume that we have a Poisson arrival process with $=0\mathrm{.}9$ customers per minute. That stream feeds two queues in series, each with a server that has $=1\mathrm{.}0$ customers per minute, as shown below.

What is the expected total time to pass through this system?

Now imagine that the Poisson arrival process has $=1\mathrm{.}8,$ but the arriving customers are randomly assigned $($with probability $1/2)$ to either of two parallel subsystems, each like the one above. The network would be as shown below. What is the expected total time to pass through this system?

Problem $3$: $($Problem $7\mathrm{.}2$ from the textbook$)$

Building on Problem $2,$ suppose that the final queues for stations $2$ and $4$ can be combined as show below $($keeping $2$ servers at the new combined station$),$ keeping all of the parameter values the same as the $4-$station problem. What is the expected total time to pass through the system now?

Problem $4$: $($Problem $7\mathrm{.}3$ from the textbook$)$

Now, suppose that the first two queues can also be merged, giving the system shown below. Keeping all of the parameter values the same, what is the expected total time to pass through this variant of the network design?

Problem $5$:$$

The above series of $3$ questions was trying to share some of the fundamental insights from networks of queues. How do these comparisons apply to queues you might experience in daily life like at the grocery store? Problem $2$: $($Question $7\mathrm{.}1$ from the textbook$)$

Assume that we have a Poisson arrival process with $\backslash (\backslash$lambda$=0\mathrm{.}9\backslash )$ customers per minute. That stream feeds two queues in series, each with a server that has $\backslash (\backslash$mu$=1\mathrm{.}0\backslash )$ customers per minute, as shown below.

$1.$ What is the expected total time to pass through this system? total time to pass through this system?

Problem $3$: $($Problem $7\mathrm{.}2$ from the textbook$)$ to pass through the system now?

Problem $4$: $($Problem $7\mathrm{.}3$ from the textbook$)$

Now, suppose that the first two queues can also be merged, giving the system shown below. Keeping all of the parameter values the same, what is the expected total time to pass through this variant of the network design?

Problem $5$:

The above series of $3$ questions was trying to share some of the fundamental insights from networks of queues. How do these comparisons apply to queues you might experience in daily life like at the grocery store?