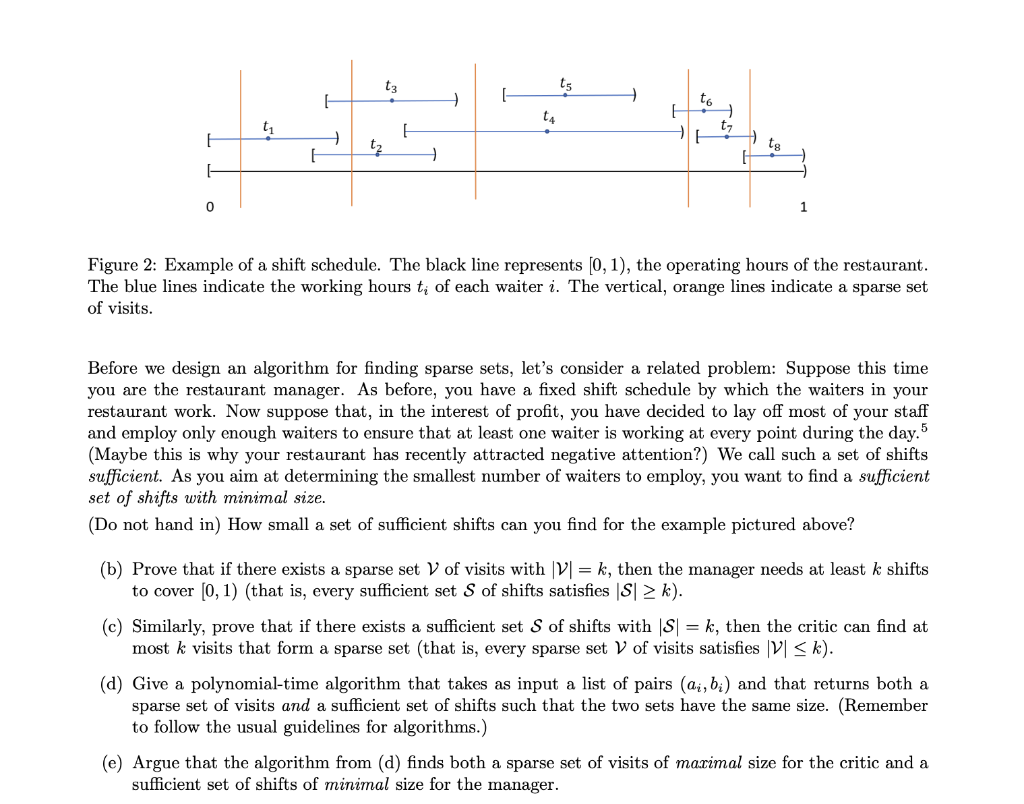
Problem 2. (Restaurant critic) You are a Michelin restaurant inspector and you have been tasked with thoroughly inspecting a 3-star restaurant that has recently come under criticism for declining dining standards. However, the restaurant knows that it is likely to be inspected. Therefore, your top priority is to hide your identity as a restaurant critic. Since you are in town for only one day, you want to visit the restaurant as many times as possible, but without encountering the same staff twice so as not to arouse suspicion. Your contact has provided you with a shift schedule of the n waiters of the restaurant, in which the working hours ti of each waiter are given as intervals ti=[ai,bi) where ai and bi are times of day. 3 For technical reasons, these time intervals are considered to be closed on the left side and open on the right side. Furthermore, we assume for simplicity that the restaurant opens at time 0 and closes at time 1 so that 0ai,bi1 for all in. Finally, we suppose that at any time in [0,1) there is at least one waiter working in the restaurant. To complete your task, you need to find the largest set of restaurant visits 4 during the day such that each waiter works during at most one visit in that set; we call a set with this property sparse. Hence, you are looking for a sparse set of visits with maximal size. The input for this problem is the list of pairs (ai,bi) for i{1,,n}. Figure 2 shows an example of a shift schedule and orange lines indicating a sparse set. Is it the largest possible sparse set? (a) Your friend suggests the following greedy approach: Sort the shifts by their starting times ai. From left to right, add point ai (the starting time of shift i ) to your set of visits, as long as it does not conflict with any previous shift (i.e., no shift covers both ai and a previously selected visit). Give an example that shows why this does not give the largest sparse set. Note: This algorithm chooses the starting times of the shifts, but a sparse set need not be restricted to those - any subset of [0,1) is fine. 1 All existing stations have been removed before you took the job, so there are currently no stations along Route 1. 2 Only stations along Route 1 count for this purpose. 3 Each waiter works only one continuous shift. 4 We suppose that a restaurant visit is instantaneous. Therefore, each restaurant visit is a single point in [0,1). Figure 2: Example of a shift schedule. The black line represents [0,1), the operating hours of the restaurant. The blue lines indicate the working hours ti of each waiter i. The vertical, orange lines indicate a sparse set of visits. Before we design an algorithm for finding sparse sets, let's consider a related problem: Suppose this time you are the restaurant manager. As before, you have a fixed shift schedule by which the waiters in your restaurant work. Now suppose that, in the interest of profit, you have decided to lay off most of your staff and employ only enough waiters to ensure that at least one waiter is working at every point during the day. 5 (Maybe this is why your restaurant has recently attracted negative attention?) We call such a set of shifts sufficient. As you aim at determining the smallest number of waiters to employ, you want to find a sufficient set of shifts with minimal size. (Do not hand in) How small a set of sufficient shifts can you find for the example pictured above? (b) Prove that if there exists a sparse set V of visits with V=k, then the manager needs at least k shifts to cover [0,1 ) (that is, every sufficient set S of shifts satisfies Sk ). (c) Similarly, prove that if there exists a sufficient set S of shifts with S=k, then the critic can find at most k visits that form a sparse set (that is, every sparse set V of visits satisfies Vk ). (d) Give a polynomial-time algorithm that takes as input a list of pairs (ai,bi) and that returns both a sparse set of visits and a sufficient set of shifts such that the two sets have the same size. (Remember to follow the usual guidelines for algorithms.) (e) Argue that the algorithm from (d) finds both a sparse set of visits of maximal size for the critic and a sufficient set of shifts of minimal size for the manager