Question: Problem # 2: Suppose that two teams play a series of games that ends when one of them has won 3 games. Suppose that each

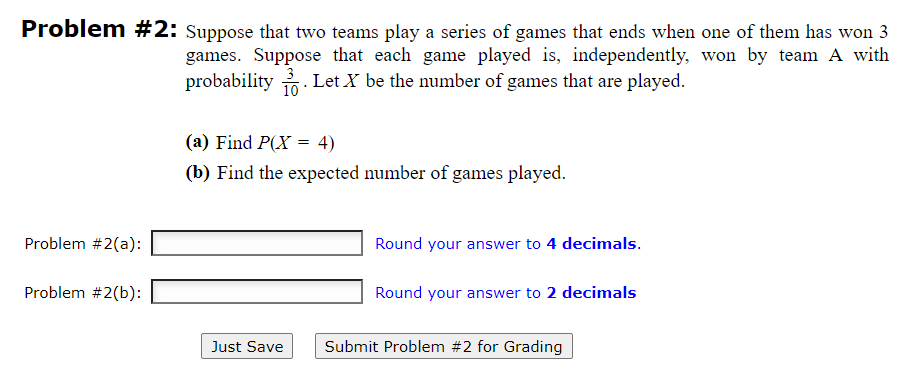
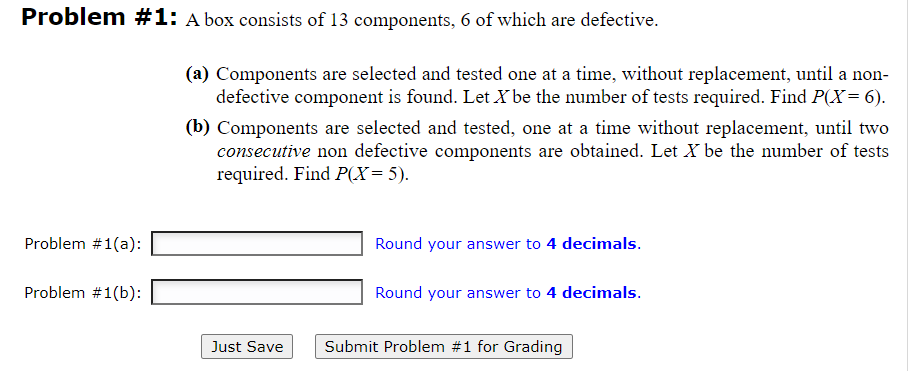
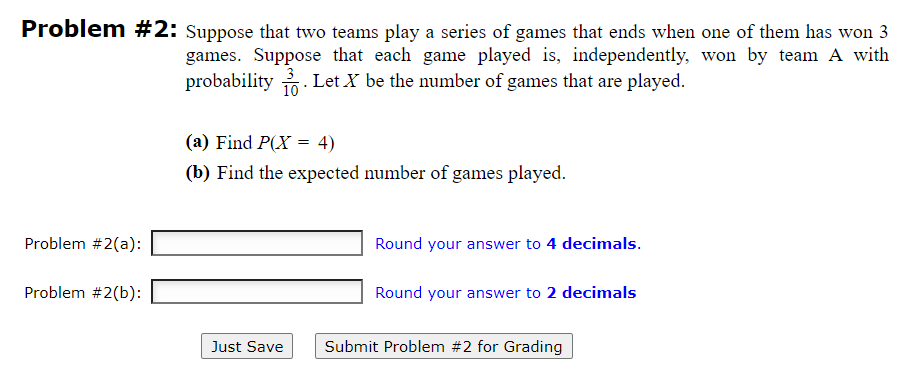
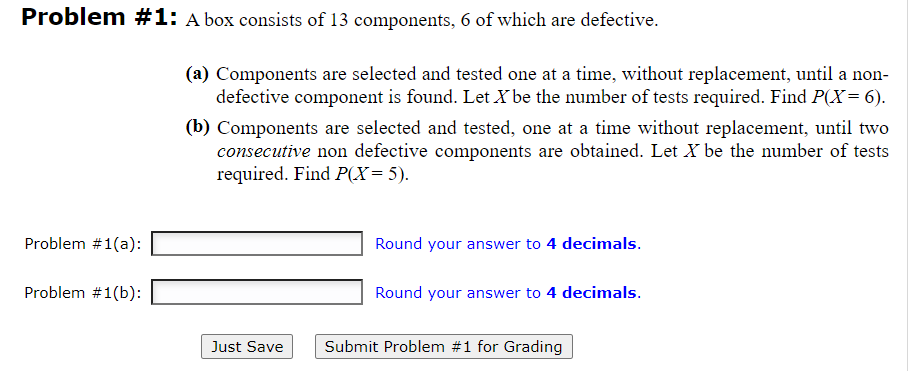
Problem # 2: Suppose that two teams play a series of games that ends when one of them has won 3 games. Suppose

that each game played is. independently. won by team A with probability

130 . Let X be the number of games that are played.

Problem # 2: Suppose that two teams play a series of games that ends when one of them has won 3 games. Suppose that each game played is. independently. won by team A with probability 130 . Let X be the number of games that are played. (3) Find P{X = 4) (b) Find the expected number of games played. Problem #2{a): |:| Round your answer to 4 decimals. Problem #2(bj: |:| Round your answer to 2 decimals Just Save Submit Problem #2 for Grading Problem # 1: A box consists of 13 components, 6 of which are defective. {3) Components are selected and tested one at a time, Twithout replacement. until a non defective component is found. Let X be the number of tests required. Find P(X= 6). ('3) Components are selected and tested, one at a time without replacement, until two consecutive non defective components are obtained. Let X be the number of tests required. Find P{X= 5}. Problem #1(aj: |:| Round your answer to 4 decimals. Problem #1(b): |:| Round your answer to 4 decimals. l Just Save I l Submit Problem #1 for Grading

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Consider Problem 22 with i = 2. Find the variance of the number of games played, and show that this number is maximized when p = 1/2. Problem 22 Suppose that two teams play a series of games that...

Suppose that two teams play a series of games that ends when one of them has won i games. Suppose that each game played is, independently, won by team A with probability p. Find the expected number...

Consider Problem 4.22 with i = 2. Find the variance of the number of games played, and show that this number is maximized when p = 1/2. Problem 4.22 Suppose that two teams play a series of games that...

1. Suppose that two teams play a series of games that ends when one of them has won 2 games. Assume that each game played is, independently, won by team A with probability , or by B with probability...

26. Suppose that two teams play a series of games that end when one of them has won i games. Suppose that each game played is, independently, won by team A with probability p. Find the expected...

Suppose that two teams play a series of games that end when one of them has won i games. Suppose that each game played is, independently, won by team A with probability p. Find the expected number of...

22. Suppose that two teams play a series of games that ends when one of them has won i games. Suppose that each game played is, independently, won by player A with probability p. Find the expected...

26. Suppose that two teams play a series of games that end when one of them has won i games. Suppose that each game played is, independently, won by team A with probability p. Find the expected...

PLEASE USE TEMPLATE PROVIDED AT THE BOTTOM OF QUESTION!!!! Human vs (Dumb) Machine A very simple way to have a program play Tic-Tac-Toe is to simply have the program pick the first empty cell to play...

2017/4/7 Section 5.6 (Part A) [43 points] 1. -/3 points A standard deck of playing cards has 52 cards, consisting of 13 "ranks" (2, 3, 4, 5, 6, 7, 8, 9, 10, jack, queen, king, ace) of each of the 4...

Disclaimer: The code that is to be written for this question MUST BE in the MIPS Assembly Language within the Mars Simulator. This is exceptionally urgent as I require a better understanding for the...

Access the Web site Webopedia. a. What is the definition given for DRM? b. What is a torrent?

Haley placed the following assets into service for her business during 2 0 2 4 : Machine, $ 2 , 0 0 0 Office desk, $ 9 0 0 Land improvement, $ 1 0 , 0 0 0 Delivery truck weighing 1 0 , 0 0 0 pounds,...

A convex mirror has a focal length of -20 cm. What is the object distance if the image distance is -10 cm?

The actual depth of a shallow pool 1.00 m deep is not the same as the apparent depth seen when you look straight down at the pool from above. How deep (in cm) will it appear to be? (nwater = 1.33.)

A plane convex lens is made of glass (n =15) with one flat surface and the other having a radius of 20 cm. What is the focal length (in cm) of the lens? O 50 O 30 O 20 O 40 O 10

If the interplanar spacing of NaCl is 2.814x1o 1 m what is the predicted angle at which X-rays of wavelength 0 140 nm will be diffracted in a first-order maximum? 10

Two harmonic waves traveling in opposite directions interfere to produce a standing wave described by y = 4 sin (5x) cos (6t) where x is in m and tis in s. What is the approximate frequency of the...

Create a 200 word summary on the Juvenile Justice System than and today. Describe The Juvenile system and provide a generalizable definition. Highlight the issues in the Juvenile system and why this...

Understanding Accounting Information 393 What balance sheet elements are different when a lease is treated as a capital lease rather than an operating lease? Why might a company wish to record a...

Multiple Choice: Noncurrent Assets Select the correct answer for each of the following. 1. Companies often are reluctant to record the costs of intangible assets as assets because: a. Outlays for...

Intangible Assets Scenter Company is considering purchasing the net assets of Ripple Corporation. Ripples reported net assets are as follows: Ripples fixed assets are depreciated on a straight-line...