*Problem 2 using MATLAB*. Problem 1 is shown for context. I also included Problem 3 from Lab 5 just to show the formatting. I am mostly struggling with c and d, so if you could explain your steps that would be great. Thank you!

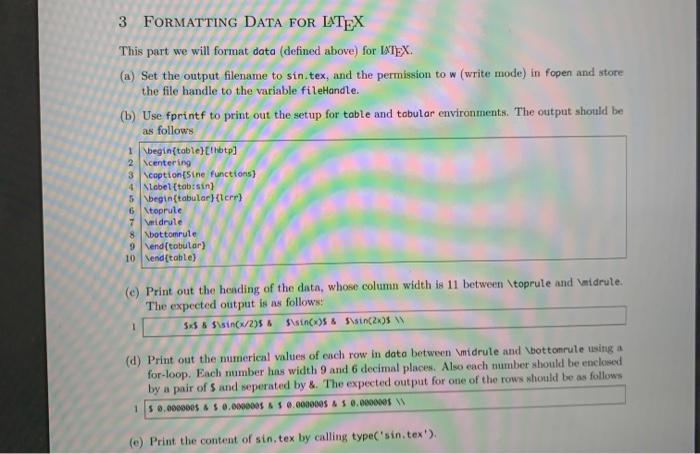
2 VARYING THE VECTOR b Suppose we want to solve the system for each integer value of m in between 0 and m-20. This time use the LU decomposition of the system matrix: perform the decomposition only once and use the lower and upper triangular factors repeatedly to find each successive solution. Then generate a table (Table 1) and a plot (Figure 1) of the solution versus the integer m. (3x +y +z = 1-5y+2: = 5 (2.1) 2x + y + 50 - 10 To do this you'll follow the steps below: (a) Define coefficient matrix A given in (2.1), and get the LU decomposition L. U of the matrix A. (b) Define a vector m which ranges from 0 to 20 with step size 1. 2 of 4 Lab OG: LU Decomposition Spring 2021 (e) Then create a for-loop, of which the loop iterator i starts from 1 to length(m). In the body of the loop, define a column vector b as the right-hand side of (2.1), where m should be the ith component of m. Then repeat () and (a) in Part 1 Store the solution to the ith row of X (d) Format the output of m and X to a file called solution, tex as you did in Part 3 of Lab 05: () Use fprintf to print out the setup for the table and tabular environments. The first column of the table is centered while the rest three columns are right-justified in INTEX (ii) Between toprule and \midrule, tise fprintf to print out the leading of the table. The column widths are 4, 11, 11, 11, respectively. (iii) Between midrule and bottomrule, use a for-loop to print each row of the table. Note that the ith row of the table consists of the ith component of m and the ith row of matrix X. The column widths are 2.9,9,9, respectively. For floating point numbers, output 6 digits after the decimal point. (iv) Call type('solution. tex') to print the content of solution.tex. (e) Plot the solution versus m using a for-loop as you did in Part 4 of Lab 05: (i) Get the size of X and assign it to XSize. Define a cell array styles, of which the entries are dashed line with hexagram, dotted line with pentagram, solid line with diamond. (ii) The use a for-loop to plot each column of X versus m in the same figure window with the above styles, (iii) Add labels, title, grid, legend as shown in Figure 1. (iv) Save the plot to a file named lab_06_plot.pdf. 1 SOLVE A SYSTEM WITH LU DECOMPOSITION (a) Define matrix A and vector bas (1.1). 21 57-26 1 2 2 -11 4 -17 45 3 -12 30 -47 4 -13 35 22 23 TA -98 30 108 200 (b) Calculate the LU decomposition L, U of the matrix A. (c) Solve the following system (1.2) and store the solution to z. Lz = b. (1.2) (d) Then solve the following system (1.3) and store the solution to x. Ux=z (1.3) (e) Check your solution by calculating the norm of the residual ||Ax - bll2 and store the result to res. 3 FORMATTING DATA FOR LATEX This part we will format data (defined above) for ITX. (a) Set the output filename to sin.tex, and the permission to w (write mode) in fopen and store the file handle to the variable fileHandle. (b) Use fprintf to print out the setup for table and tabular environments. The output should be as follows 1 \begin{table) thotpl 2 Scentering 3 coption (Sine functions) 4 Label (tab:sin) 5 \begin{tabular Herr 6 Ntoprute 7 Widrule Xbottomrute 9 Vend(tobular) 10 end (table) (e) Print out the heading of the data, whose column width is 11 between \toprule and Imidrule. The expected output is as follows: $$ & S\sin(x/295 $ SOOS & $\sin(2) W (d) Print out the numerical values of ench row in data between \midrule and bottonrule using a for-loop. Each number has width 9 and 6 decimal places. Also each number should be enclosed by a pair of sand seperated by &. The expected output for one of the rows should be as follows 15 0.000000$ 0.00000055 0.000000 $ 0.000000 (e) Print the content of sin.tex by calling type'sin.tex'). 2 VARYING THE VECTOR b Suppose we want to solve the system for each integer value of m in between 0 and m-20. This time use the LU decomposition of the system matrix: perform the decomposition only once and use the lower and upper triangular factors repeatedly to find each successive solution. Then generate a table (Table 1) and a plot (Figure 1) of the solution versus the integer m. (3x +y +z = 1-5y+2: = 5 (2.1) 2x + y + 50 - 10 To do this you'll follow the steps below: (a) Define coefficient matrix A given in (2.1), and get the LU decomposition L. U of the matrix A. (b) Define a vector m which ranges from 0 to 20 with step size 1. 2 of 4 Lab OG: LU Decomposition Spring 2021 (e) Then create a for-loop, of which the loop iterator i starts from 1 to length(m). In the body of the loop, define a column vector b as the right-hand side of (2.1), where m should be the ith component of m. Then repeat () and (a) in Part 1 Store the solution to the ith row of X (d) Format the output of m and X to a file called solution, tex as you did in Part 3 of Lab 05: () Use fprintf to print out the setup for the table and tabular environments. The first column of the table is centered while the rest three columns are right-justified in INTEX (ii) Between toprule and \midrule, tise fprintf to print out the leading of the table. The column widths are 4, 11, 11, 11, respectively. (iii) Between midrule and bottomrule, use a for-loop to print each row of the table. Note that the ith row of the table consists of the ith component of m and the ith row of matrix X. The column widths are 2.9,9,9, respectively. For floating point numbers, output 6 digits after the decimal point. (iv) Call type('solution. tex') to print the content of solution.tex. (e) Plot the solution versus m using a for-loop as you did in Part 4 of Lab 05: (i) Get the size of X and assign it to XSize. Define a cell array styles, of which the entries are dashed line with hexagram, dotted line with pentagram, solid line with diamond. (ii) The use a for-loop to plot each column of X versus m in the same figure window with the above styles, (iii) Add labels, title, grid, legend as shown in Figure 1. (iv) Save the plot to a file named lab_06_plot.pdf. 1 SOLVE A SYSTEM WITH LU DECOMPOSITION (a) Define matrix A and vector bas (1.1). 21 57-26 1 2 2 -11 4 -17 45 3 -12 30 -47 4 -13 35 22 23 TA -98 30 108 200 (b) Calculate the LU decomposition L, U of the matrix A. (c) Solve the following system (1.2) and store the solution to z. Lz = b. (1.2) (d) Then solve the following system (1.3) and store the solution to x. Ux=z (1.3) (e) Check your solution by calculating the norm of the residual ||Ax - bll2 and store the result to res. 3 FORMATTING DATA FOR LATEX This part we will format data (defined above) for ITX. (a) Set the output filename to sin.tex, and the permission to w (write mode) in fopen and store the file handle to the variable fileHandle. (b) Use fprintf to print out the setup for table and tabular environments. The output should be as follows 1 \begin{table) thotpl 2 Scentering 3 coption (Sine functions) 4 Label (tab:sin) 5 \begin{tabular Herr 6 Ntoprute 7 Widrule Xbottomrute 9 Vend(tobular) 10 end (table) (e) Print out the heading of the data, whose column width is 11 between \toprule and Imidrule. The expected output is as follows: $$ & S\sin(x/295 $ SOOS & $\sin(2) W (d) Print out the numerical values of ench row in data between \midrule and bottonrule using a for-loop. Each number has width 9 and 6 decimal places. Also each number should be enclosed by a pair of sand seperated by &. The expected output for one of the rows should be as follows 15 0.000000$ 0.00000055 0.000000 $ 0.000000 (e) Print the content of sin.tex by calling type'sin.tex')