Problem $2$

Write a function called decrypt that accepts three numbers $(c,m,$ and $k)$ and returns the corresponding plaintext $(p)$ value Greatest Common Divisor, Extended Euclidean Algorithm$$

In Lesson $6$ you learned about the Euclidean Algorithm for computing the greatest common divisor. And in a recent lecture we learned about the Extended Euclidean Algorithm for computing the more general form of the greatest common divisor: $+=$gcd$(,)$

$.$

The solution to this equation is a pair $($a tuple$)$ of integers $($x$,$ y$).$

Here is a recursive definition by parts of the Extended Euclidean Algorithm, which I will call egcd:

egcd$(,)=(1,0)(,)$if $=0,$otherwise, where$=-$:$(,)=$egcd$(,$mod$)$q is the integer quotient

Let's turn this into a Python function. I've given you some hints in the comments below.

def egcd$($a$,$ b$)$:

if b $==0$:

return $(1,0)$

else:

q $=$ a $//$ b

$($s$,$ t$)=$ egcd$($b$,$ a $\%$ b$)$

return $($t$,$ s $-$ q $*$ t$)$

# Run this cell to check your egcd function

assert egcd$(5,37)==(15,-2)$

assert egcd$(81,256)==(-79,25)$

Multiplicative Inverse

To be able to decrypt a linear cipher, we need to solve the following equation for p:

$=+($mod$)$

After a little algebraic manipulation, we get

$=($mod$)$

But dividing by m would result in a fraction. Instead of dividing, we can multiply by the multiplicative inverse of m $($mod n$).$ Recall that $1($mod $)$

is the nomenclature for the multiplicative inverse of m mod n$.$ We rewrite the equation as:

$=()1($mod$)$

To compute the multiplicative inverse, we'll use the Extended Euclidean Algorithm! Recall that it returns the $($x$,$ y$)$ solution to $+=$gcd$(,)$

$.$ It turns out that x is the multiplicative inverse of a mod b$.$

Therefore, if we call egcd$($m$,$ n$)$ and get back the tuple $($x$,$ y$),$ the multiplicative inverse is just the x value.

Sometimes you get back a negative value for x; that's okay, but a positive integer would be better. To convert it to the congruent positive modular value, just do a final mod n$.$ For example, if we were trying to compute the multiplicative inverse of $5$ mod $37$ and we got back $22,$ we could just calculate $22$ mod $37$ and return the desired value, $15,$ to the caller.

To write the Python function, simply call egcd$($a$,$ n$),$ obtain the first element of the tuple that you get back, do a final mod n on it and return the result.

With that working, we will be ready to decrypt the linear cipher!

Problem $1$

Write the multinv function. It takes two numbers, a and n$,$ and returns the multiplicative inverse of $$mod$$

$.$ There are comments in the function below to help you.

def multinv$($a$,$ n$)$:

# Call egcd$($a$,$ n$)$ and get back a pair of integers $($x$,$ y$)$

$($x$,$ y$)=$ egcd$($a$,$ n$)$

# Return the first element $($the x value$),$ modulo n

return x $\%$ n

# Run this cell to check your multinv function

assert multinv$(18,47)==34$

assert multinv$(81,256)==177$

assert multinv$(5,37)==15$

# Try it out! This should return $177$

multinv$(81,256)$

$203$

# Verify $81*177$ mod $256.$ This should return $1$

$81*$ multinv$(81,256)\%256$

$59$

Decrypting the Linear Cipher

The functions you'll write below are similar to the ones you wrote for Lab $4,$ except they decrypt instead of encrypt. You may want to open up that notebook and refer to them.

If all this seems daunting to you, relax. You have the pieces you need to write the functions; you just have to put them together. An essential aspect of problem$-$solving is taking inventory of what you already know and what you have available to use.

You've learned about lists and applying functions to elements of a list using map.

You know about byte strings: special arrays of integers that appear on$-$screen kind of like strings.

You know that byte strings can be accessed like lists; you can loop across them. Python's map makes this very easy.

You have a working function for calculating the mutiplicative inverse of an integer.

These are all the pieces you need to finish the programs. None of the functions below are more than one or two lines of code.

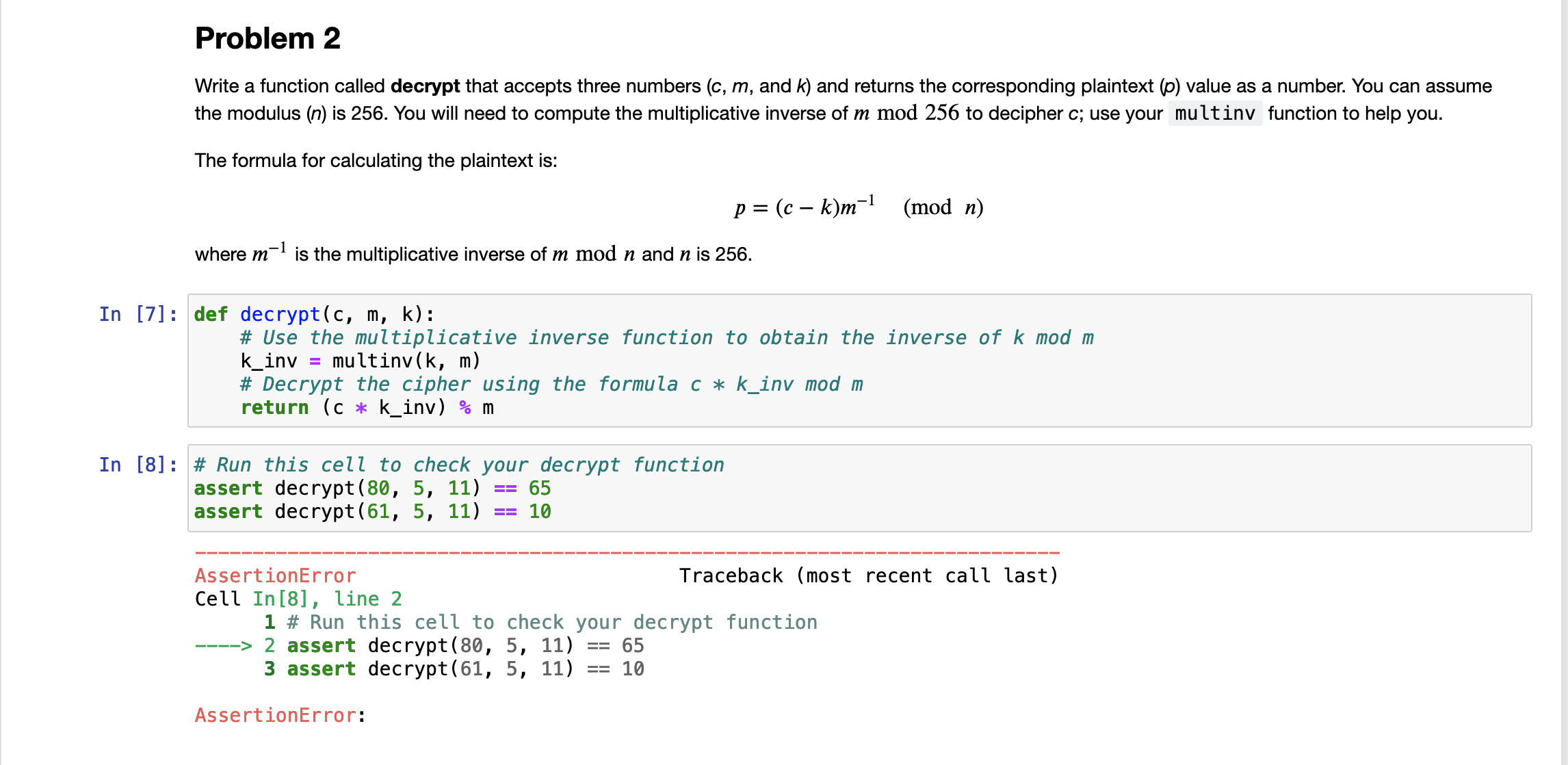
Problem $2$

Write a function called decrypt that accepts three numbers $($c$,$ m$,$ and k$)$ and returns the corresponding plaintext $($p$)$ value as a number. You can assume the modulus $($n$)$ is $256.$ You will need to compute the multiplicative inverse of $$mod$256$

to decipher c; use your multinv function to help you.

The formula for calculating the plaintext is:

$=()1($mod$)$

where $1$

is the multiplicative inverse of $$mod$$ and $$

is $256.$

def decrypt$($c$,$ m$,$ k$)$:

# Use the multiplicative inverse function to obtain the inverse of k mod m

k$\_$inv $=$ multinv$($k$,$ m$)$

# Decrypt the cipher using the formula c $*$ k$\_$inv mod m

return $($c $*$ k$\_$inv$)\%$ m

# Run this cell to check your decrypt function

assert decrypt$(80,5,11)==65$

assert decrypt$(61,5,11)==$

$---->2$ assert decrypt$(80,$