Problem 2.1 Area of triangle

Consider two points in 3d, and . Show that the area of the triangle spanned by , and the origin in terms of the components of these vectors is given by

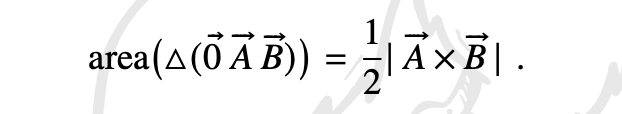
\fExample 2.1.2: Rockets Let us discuss how rock- ets accelerate. To this end, consider momen- tum conservation. The rocket hurl burnt fuel in the opposite direction that it wants to y in. Since total momentum is conserved, the rocket accelerates. Turn this into equations. Figure 2.2: Cartoon of a rocket. This is a l-dimensional problem. The momentum of the rocket is PU) = m(t)V(t) , where m(t) is the mass of the rocket. This function m(t) decreases with time since the rocket loses the mass of the fuel it burns off. The momentum, PU), of the rocket alone is not preserved. What is preserved instead is the total momentum. At a given time, the fuel hurled out by the rocket has momentum Am(v(t) vex) . Since Am = mm in the limit At > O, we can recast momentum conservation as . l where we have used the product rule and stopped to indicate the time-dependence explicitly. Therefore, mi) = m vex . (2.3) The right-hand side of this equation is known as thrust, thrust := rh vex . Equation (2.3) tells us that the acceleration of the rocket is given by the product of the amount of fuel it burns per time and the relative velocity the fuel gets hurled out